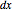Quantum Motion of Two Particles in a 3D Trigonometric Pöschl-Teller Potential

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Exact solutions of the nonrelativistic wave equations contain all the necessary information for the quantum system and have important applications in particle physics. This Demonstration discusses a solution of the Schrödinger equation in three-dimensional configuration space with the trigonometric Pöschl–Teller potential in the Bohm approach.
[more]
Contributed by: Klaus von Bloh (March 2015)
Open content licensed under CC BY-NC-SA
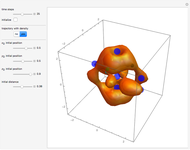
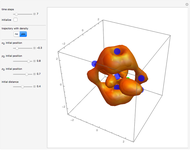
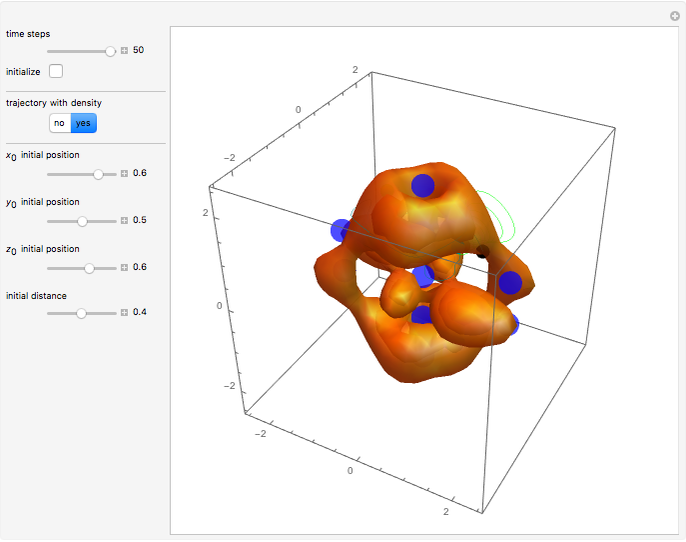
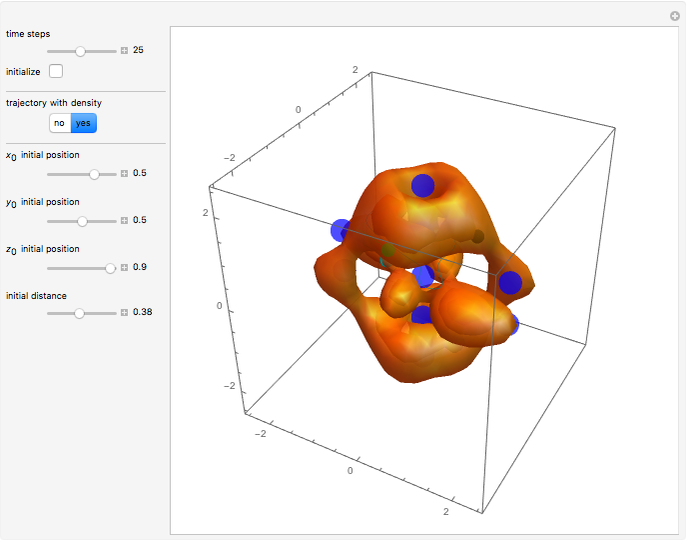
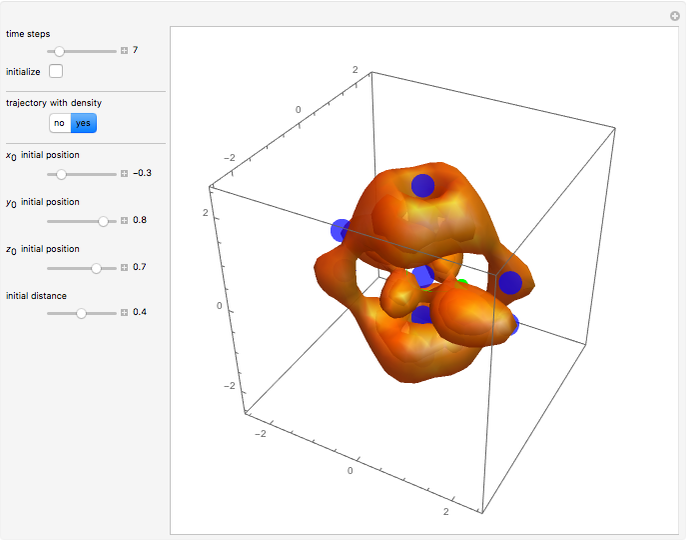
Snapshots
Details
Associated Legendre polynomials arise as the solution of the Schrödinger equation:
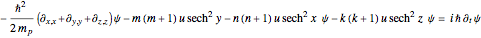 ,
,
with the integers 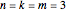 ,
, 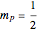 ,
, 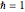 ,
, 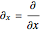 , and so on. A degenerate, unnormalized wavefunction
, and so on. A degenerate, unnormalized wavefunction  with time period
with time period 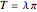 for
for 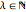 for the three-dimensional case can be expressed by:
for the three-dimensional case can be expressed by:
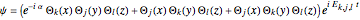 ,
,
where 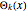 ,
, 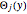 ,
, 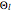
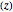 are eigenfunctions, and
are eigenfunctions, and 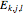 are permuted eigenenergies of the corresponding stationary one-dimensional Schrödinger equation with
are permuted eigenenergies of the corresponding stationary one-dimensional Schrödinger equation with 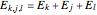 . The eigenfunctions are defined by
. The eigenfunctions are defined by
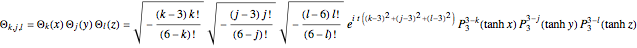 ,
,
where  ,
,  ,
, 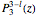 are associated Legendre polynomials. The parameter
are associated Legendre polynomials. The parameter  is a constant phase shift
is a constant phase shift  , and
, and 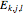 are the quantum numbers
are the quantum numbers 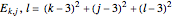 with
with 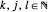 and
and 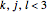 . The wavefunction is taken from [2].
. The wavefunction is taken from [2].
For this Demonstration, the wavefuction  is defined by:
is defined by:
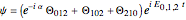 .
.
Due to the permuted wavefunction structure and depending on the constant phase shift  , most of the nodal points are positioned only in the
, most of the nodal points are positioned only in the  ,
,  plane.
plane.
The velocity field 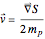 is calculated from the gradient of the phase from the total wavefunction in the eikonal form (often called polar form)
is calculated from the gradient of the phase from the total wavefunction in the eikonal form (often called polar form) 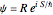 . The time-dependent phase function
. The time-dependent phase function 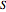 from the total wavefunction
from the total wavefunction  is:
is:
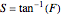 , with
, with
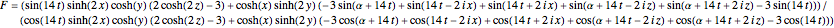 .
.
The corresponding velocity field becomes time independent (autonomous) because of the gradient of the phase function.
The velocity in the  direction becomes zero if
direction becomes zero if 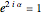 , which is fulfilled for
, which is fulfilled for 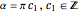 . The velocities in the other directions become zero for
. The velocities in the other directions become zero for 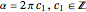 . The length of the curve depends on the constant phase shift
. The length of the curve depends on the constant phase shift  .
.
In the program, if PlotPoints, AccuracyGoal, PrecisionGoal, and MaxIterations are increased, the results will be more accurate.
References
[1] G. Pöschl, E. Teller, "Bemerkungen zur Quantenmechanik des anharmonischen Oszillators," Zeitschrift für Physik, 83 (3–4), 1933 pp. 143–151. doi:10.1007/BF01331132.
[2] M. Trott, The Mathematica GuideBook for Symbolics, New York: Springer-Verlag, 2006.
[3] "Bohmian-Mechanics.net." (Mar 16, 2015) www.bohmian-mechanics.net/index.html.
[4] S. Goldstein. "Bohmian Mechanics." The Stanford Encyclopedia of Philosophy. (Mar 16, 2015)plato.stanford.edu/entries/qm-bohm.
[5] K. von Bloh. The Quantum Motion of Eight Particles in a 3D Trigonometric Pöschl–Teller Potential. [Video]. (Mar 16, 2015) www.youtube.com/watch?v=ejJF3cSWa4Y.
Permanent Citation