Quasi-Exact Solutions of Schrödinger Equation: Sextic Anharmonic Oscillator

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
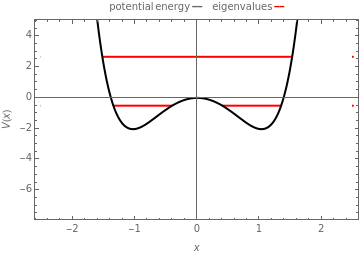
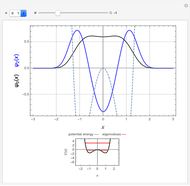
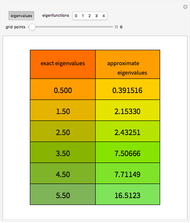
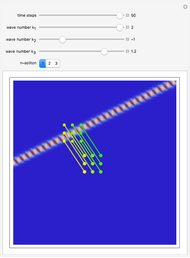
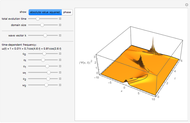
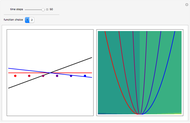
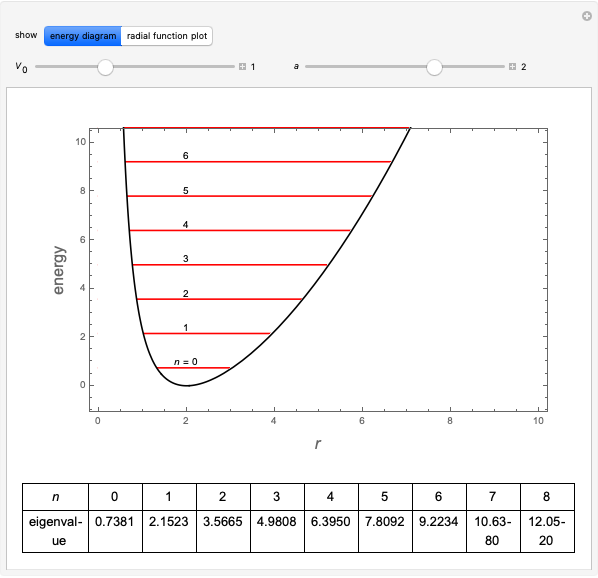
Quasi-exact solutions to a Schrödinger equation pertain to limited regions of a spectrum of eigenstates for which closed-form eigenfunctions and eigenvalues can be derived, whereas the remainder of the spectrum can only be approximated. These occur for certain potentials with parameters in some limited range. The sextic anharmonic oscillator is the only one-dimensional polynomial potential that can be quasi-exactly solved if its parameters are appropriately chosen. Depending on the parameters, the system can be a single-, double- or triple-well potential.
[more]
Contributed by: S. M. Blinder (April 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For simplicity, set  . For
. For  ,
,
 .
.
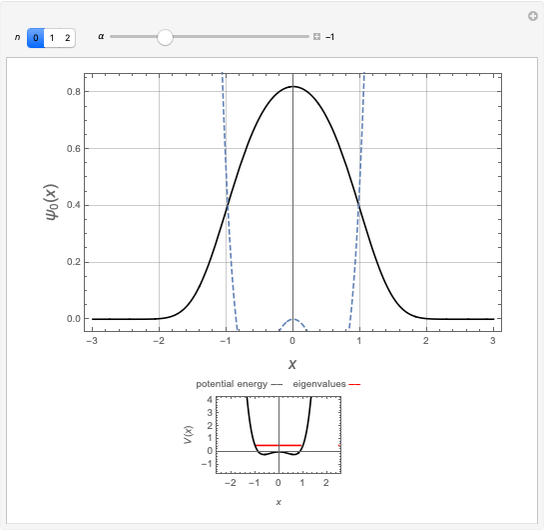
The ground state  is quasi-exactly soluble:
is quasi-exactly soluble:
 ,
,  ,
,
 .
.
For  ,
,
 .
.
The first-excited state  is quasi-exactly soluble:
is quasi-exactly soluble:
 ,
,  ,
,
 .
.
For  ,
,
 .
.
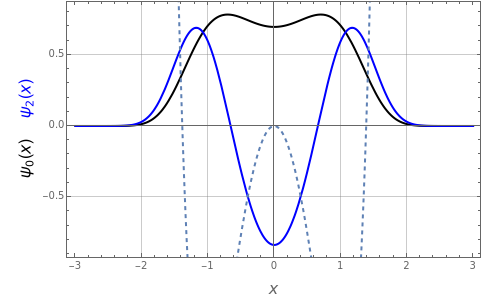
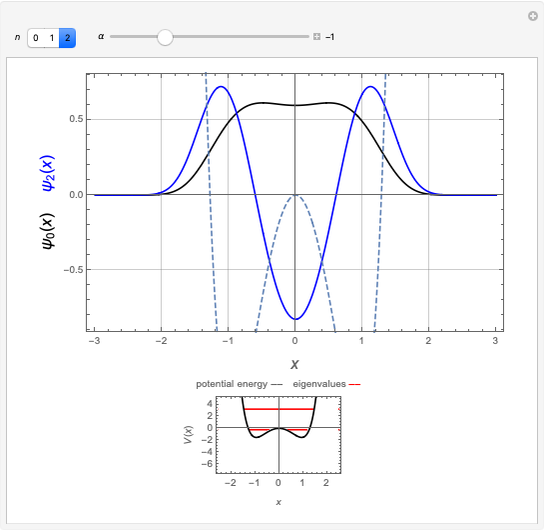
The ground state  and the second-excited state
and the second-excited state  are quasi-exactly soluble:
are quasi-exactly soluble:
 ,
,  ,
,
 ,
,  ,
,
 .
.
References
[1] A. V. Turbiner, "One-Dimensional Quasi-exactly Solvable Schrödinger Equations," Physics Reports, 642, 2016 pp. 1–71. doi:10.1016/j.physrep.2016.06.002.
[2] S. Konstantogiannis, "Quasi-exact Solution of Sextic Anharmonic Oscillator Using a Quotient Polynomial," Journal for Foundations and Applications of Physics, 6(1), 2019 pp. 17–34. sciencefront.org/ojs/index.php/jfap/article/view/109.
Permanent Citation