Quaternion Addition and Multiplication

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
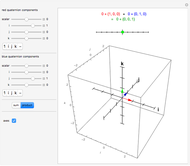
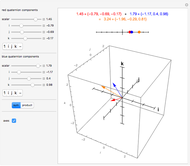
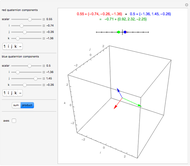
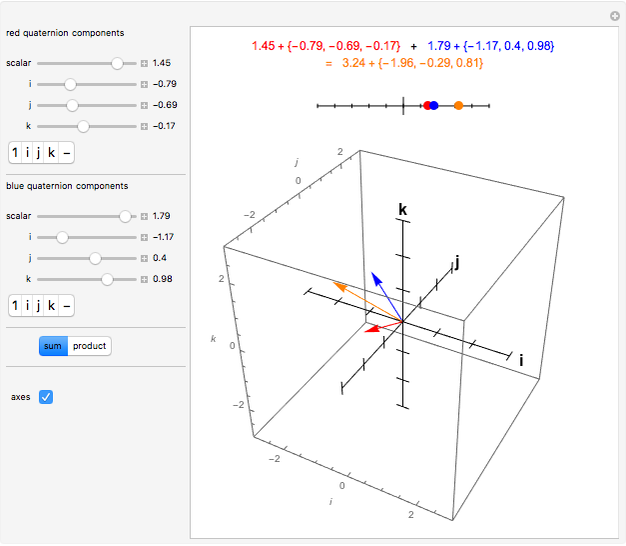
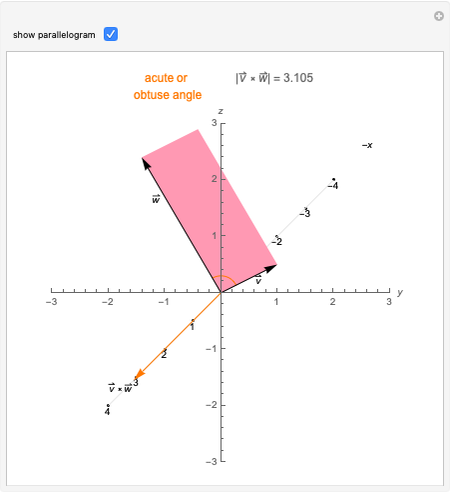
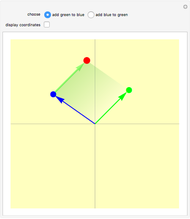
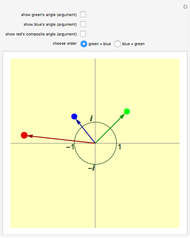
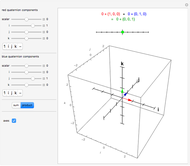
The quaternions are a number system with a noncommutative multiplication denoted here by *. They can be represented in various ways: as pairs of complex numbers, as four-dimensional vectors with real components, or as the sum of a real scalar and a real three-dimensional vector, as is done in this Demonstration. The scalar part of the quaternion is shown on a line and the vector part is shown in 3D.
[more]
Contributed by: Jon Perry (November 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Write a quaternion as a scalar plus a three-vector,  .
.
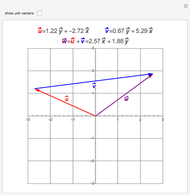
Quaternion addition is component-wise:  .
.
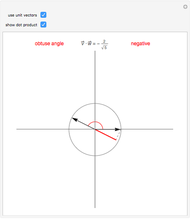
Quaternion multiplication is defined by  , where . is the vector dot product and
, where . is the vector dot product and  is the vector cross product.
is the vector cross product.
Snapshot 1:  , but
, but 
Permanent Citation