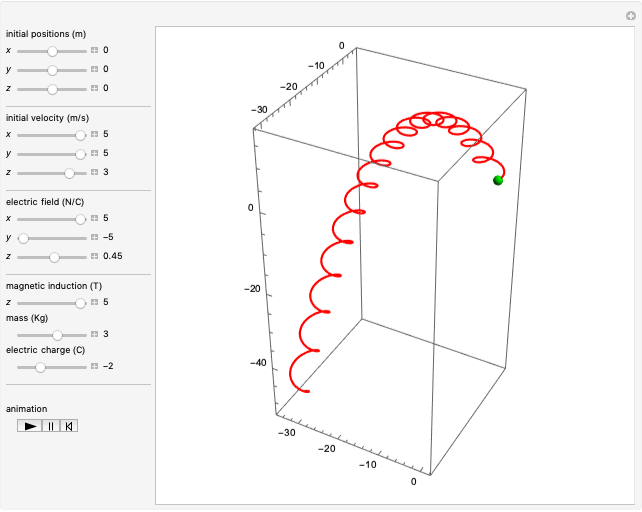
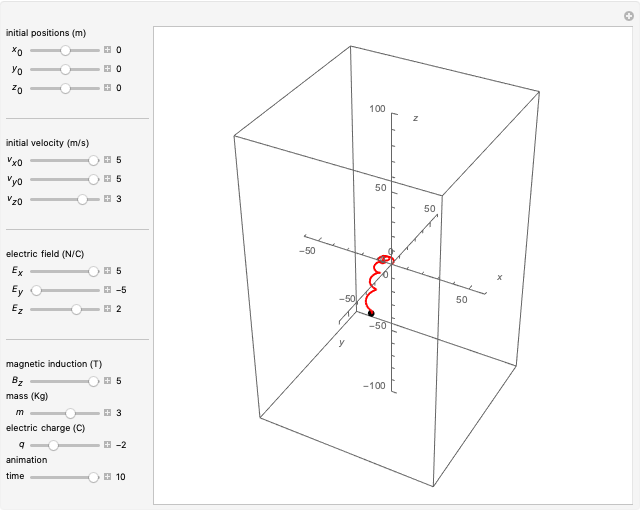
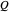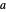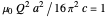Radiation Pattern from Accelerated Point Charge

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
A charged particle produces an electric field and, when in motion, also a magnetic field. Furthermore, if accelerated, the particle emits electromagnetic radiation at the speed of light  .
.
Contributed by: Deyvid W. M. Pastana, Manuel E. Rodrigues and Luciano J. B. Quaresma (December 2020)
Open content licensed under CC BY-NC-SA
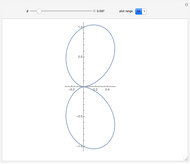
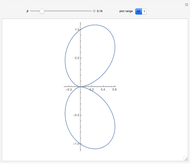
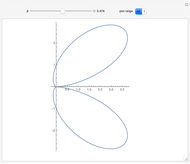
Snapshots
Details
Start with the Liénard–Wiechert potentials for a point particle with charge 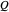 in arbitrary motion:
in arbitrary motion:
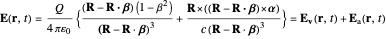
and
 ,
,
where
 ,
,
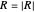 ,
,
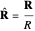 ,
,
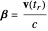 ,
,
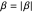 ,
,
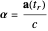
and
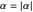 .
.
The electric field has two terms, one determined by the velocity 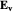 and the other by the acceleration
and the other by the acceleration 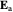 , proportional to
, proportional to 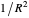 and
and  , respectively. Because at large distances the acceleration terms dominate, these are also known as radiation fields. The Poynting vector is given by
, respectively. Because at large distances the acceleration terms dominate, these are also known as radiation fields. The Poynting vector is given by
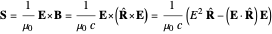 ,
,
which represents the energy flux due to the electromagnetic field of the particle in motion. Some of the energy stays with the particle, while the remainder represents emitted radiation.
Consider a sphere of radius 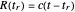 centered on the particle in the retarded time; the radiation reaches its surface an instant
centered on the particle in the retarded time; the radiation reaches its surface an instant  after being emitted at
after being emitted at 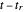 . As the area of a sphere grows proportionally to
. As the area of a sphere grows proportionally to 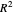 , only the terms of the radiation field become relevant, as noted. In this case, the radiation field is perpendicular to
, only the terms of the radiation field become relevant, as noted. In this case, the radiation field is perpendicular to 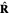 so the second term in the Poynting vector is zero and we have
so the second term in the Poynting vector is zero and we have
 .
.
The radiation power passing through an element of the surface of the sphere on an instant  is, in terms of a solid angle,
is, in terms of a solid angle,
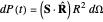 .
.
This power is not the same as that produced by the charge at 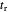 ; rather it is
; rather it is
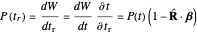 ,
,
so the radiated power per unit of solid angle produced is
 .
.
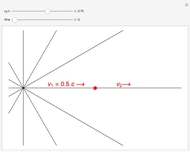
The goal of this Demonstration is to find the behavior of the radiation emitted by a point charge with colinear acceleration and velocity. In this case, 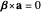 and
and
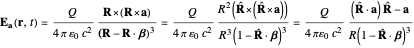 .
.
The Poynting vector is therefore
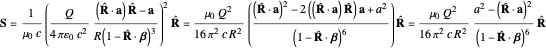
and defining  as the angle between
as the angle between 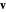 and
and  , from
, from 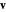 , the acceleration could be parallel or antiparallel so the angle between
, the acceleration could be parallel or antiparallel so the angle between  and
and 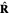 could be
could be  or
or 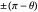 , but
, but 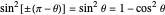 , so this does not modify the result
, so this does not modify the result
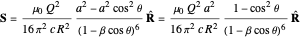 .
.
Finally, the radiated power per unit of solid angle is
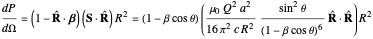 ,
,
which gives
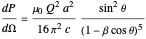 .
.
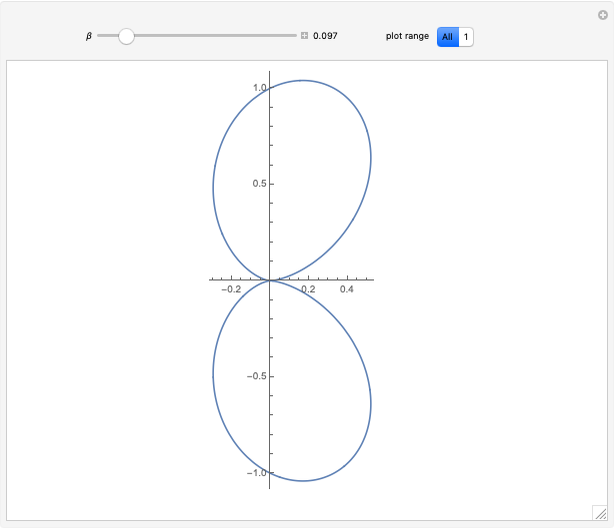
In this Demonstration, assume  for simplification.
for simplification.
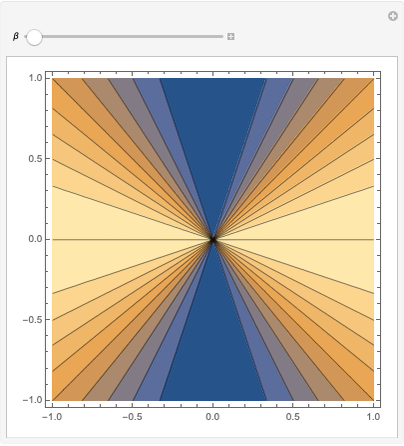
This equation implies that as 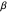 increases, the radiation is emitted preferentially toward the direction of the particle motion, even if the particle is being decelerated, with
increases, the radiation is emitted preferentially toward the direction of the particle motion, even if the particle is being decelerated, with 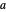 negative. For example, when a high-energy electron is deflected by an atomic nucleus, it emits radiation known as Bremsstrahlung, which can be described by the equations in this Demonstration.
negative. For example, when a high-energy electron is deflected by an atomic nucleus, it emits radiation known as Bremsstrahlung, which can be described by the equations in this Demonstration.
References
[1] K. D. Machado, Teoria do Eletromagnetismo, Vol. 3, Ponta Grossa, Brazil: UEPG, 2006.
[2] J. D. Jackson, Classical Electrodynamics, 3rd ed., New York: Wiley, 1999.
[3] D. J. Griffiths, Introduction to Electrodynamics, 4th ed., Boston: Pearson, 2013.
Permanent Citation