Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

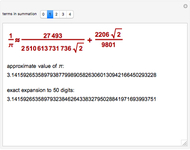
Ramanujan's Strange Formula for Pi

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

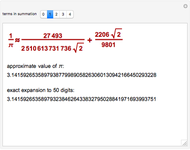
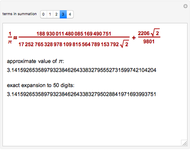
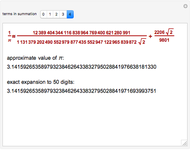
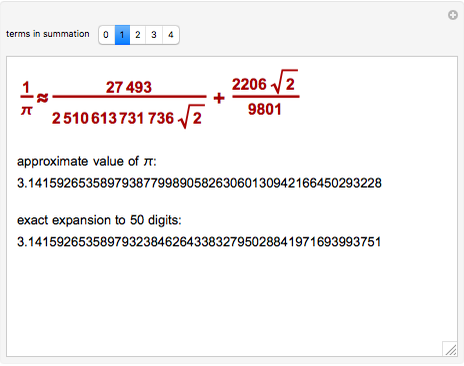
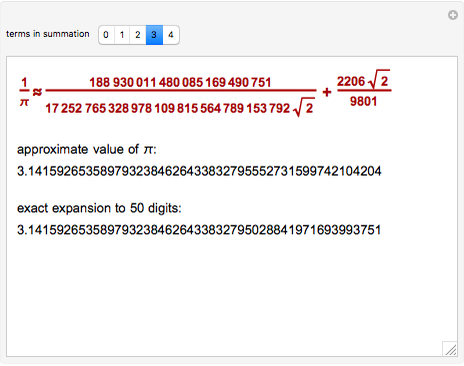
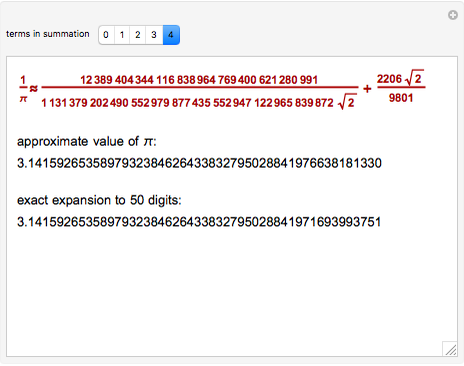
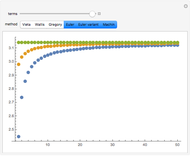
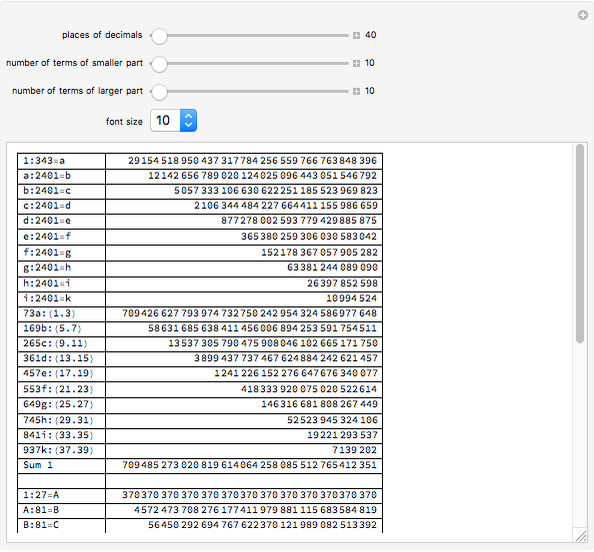
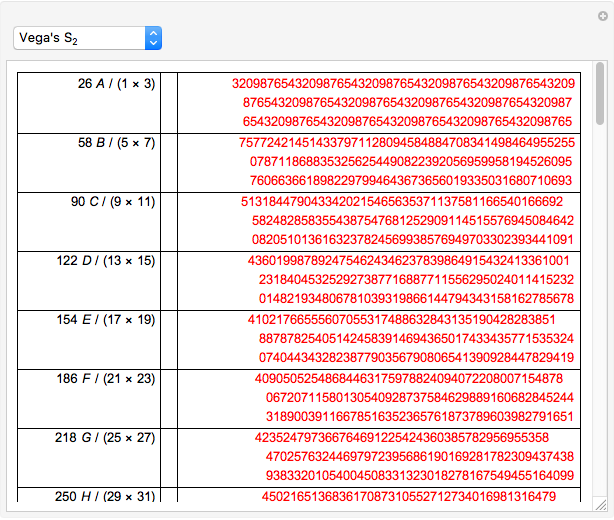
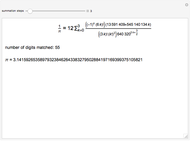
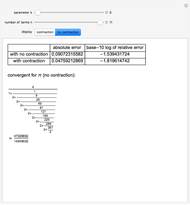
Finding an accurate approximation to has been one of the most noteworthy challenges in the history of mathematics. Srinivasa A. Ramanujan (1887–1920), a mathematical thinker of phenomenal abilities, discovered a mysterious infinite series for estimating the value of [1]:

[more]

.

The series is known to be a specialization of a modular equation of order 58 [2].

This Demonstration gives numerical estimates for using the reciprocal of the series up to , which gives a correct approximation to 38 decimal places.

[less]

Contributed by: Allan Zea (February 2017)
Suggested by: Dr. Jean Carlos Liendo
Open content licensed under CC BY-NC-SA

Snapshots

Details

References

[1] S. Ramanujan, "Modular Equations and Approximations to ," The Quarterly Journal of Mathematics, 45, 1914 pp. 350–372.

[2] J. M. Borwein, P. B. Borwein and D. H. Bailey, "Ramanujan, Modular Equations, and Approximations to Pi or How to Compute One Billion Digits of Pi," The American Mathematical Monthly, 96(3), 1989 pp. 201–219. doi:10.2307/2325206.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send