Random Walks Based on Continued Fraction Expansions of Real Numbers

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
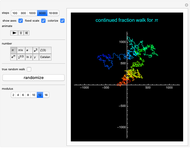
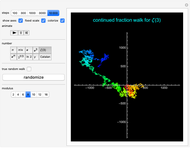
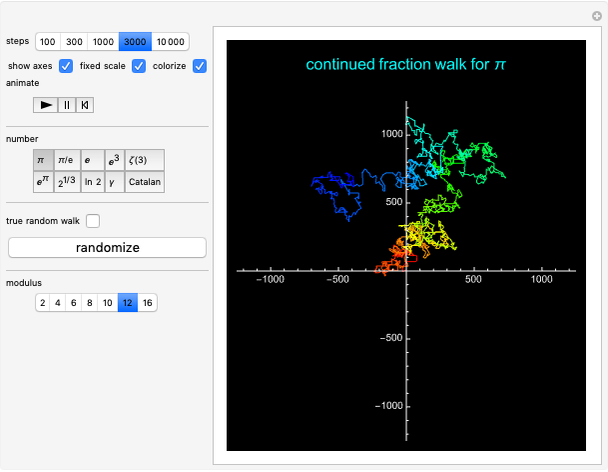
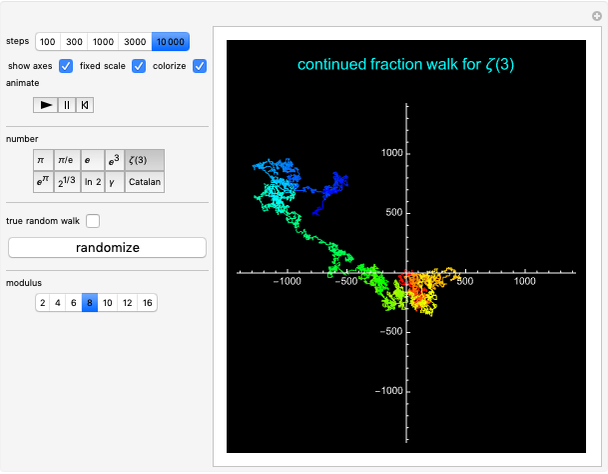
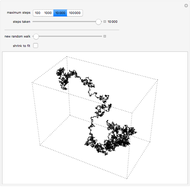
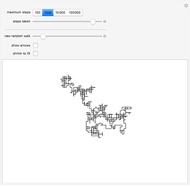
The sequence of digits in the simple continued fraction expansion of  and many other famous irrational numbers is conjectured to behave randomly in an appropriate sense. This Demonstration illustrates this behavior by constructing walks based on the continued fraction digits of a number and comparing these walks to similar true random walks.
and many other famous irrational numbers is conjectured to behave randomly in an appropriate sense. This Demonstration illustrates this behavior by constructing walks based on the continued fraction digits of a number and comparing these walks to similar true random walks.
Contributed by: Alex Jin, Efstathios Konstantinos Chrontsios Garitsis and A. J. Hildebrand. (August 2022)
(Based on an undergraduate research project at the Illinois Geometry Lab in Spring 2022.)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration was inspired by [1], on the construction of two-dimensional walks from continued fraction expansions of selected real numbers. Given a real number  and a base
and a base  , the walk begins at the origin with the
, the walk begins at the origin with the  step of length 1 in the direction
step of length 1 in the direction 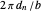 , where
, where 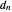 is the
is the 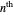 digit in the base
digit in the base  expansion of
expansion of  .
.
To construct analogous walks based on the sequence of continued fraction digits of  (i.e. the partial quotients in the continued fraction expansion of
(i.e. the partial quotients in the continued fraction expansion of  ), we fix a modulus
), we fix a modulus 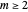 and reduce the continued fraction digits modulo
and reduce the continued fraction digits modulo 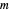 to obtain a sequence of reduced digits with values in
to obtain a sequence of reduced digits with values in  . This sequence is then mapped to a sequence of steps in a walk by mapping a reduced digit
. This sequence is then mapped to a sequence of steps in a walk by mapping a reduced digit  to a step in the direction
to a step in the direction 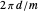 of length
of length 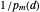 . Here
. Here 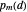 is an appropriate normalizing factor since, unlike the digits in the usual base
is an appropriate normalizing factor since, unlike the digits in the usual base  expansion of a typical real number
expansion of a typical real number  , the reduced continued fraction digits do not have uniform probabilities. Specifically, a positive integer
, the reduced continued fraction digits do not have uniform probabilities. Specifically, a positive integer  appears in the continued fraction expansion of a typical real number
appears in the continued fraction expansion of a typical real number  with frequency given by the Gauss–Kuzmin distribution (see, for example, [2, Section 3.4] or [3, Section 15])
with frequency given by the Gauss–Kuzmin distribution (see, for example, [2, Section 3.4] or [3, Section 15])
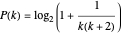 .
.
Therefore, the proportion of continued fraction digits that are congruent to  modulo
modulo  is given by
is given by
 .
.
Choosing steps of length 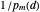 ensures that the resulting walk has no drift.
ensures that the resulting walk has no drift.
The case 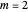 is mapped to a one-dimensional walk with steps
is mapped to a one-dimensional walk with steps 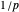 and
and 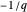 , where
, where  and
and 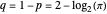 . This walk can be visualized using ListLinePlot to show the position of the walk after
. This walk can be visualized using ListLinePlot to show the position of the walk after  steps, as a function of
steps, as a function of 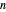 . When
. When 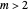 , we obtain a two-dimensional walk in the plane, with steps given as described above.
, we obtain a two-dimensional walk in the plane, with steps given as described above.
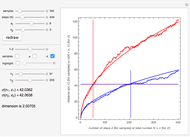
While the continued fraction expansion of 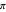 and other famous mathematical constants is conjectured to behave like that of a typical real number
and other famous mathematical constants is conjectured to behave like that of a typical real number  , there are some notable exceptions. In particular, quadratic irrationals have a periodic continued fraction expansion, and certain transcendental numbers have an expansion that follows a predictable pattern. For example, the continued fraction expansion of
, there are some notable exceptions. In particular, quadratic irrationals have a periodic continued fraction expansion, and certain transcendental numbers have an expansion that follows a predictable pattern. For example, the continued fraction expansion of  is
is 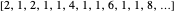 (see, for example, [2, Appendix A.1]). This regularity is reflected in the continued fraction digit walk based on
(see, for example, [2, Appendix A.1]). This regularity is reflected in the continued fraction digit walk based on  : the walk has a noticeable drift and is clearly nonrandom. By contrast, walks based on
: the walk has a noticeable drift and is clearly nonrandom. By contrast, walks based on 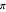 and most other non-quadratic irrationals behave like true random walks constructed from a sequence of independent random digits following the Gauss–Kuzmin distribution.
and most other non-quadratic irrationals behave like true random walks constructed from a sequence of independent random digits following the Gauss–Kuzmin distribution.
The controls provide the following options:
1. The "steps" setter bar sets the number of steps of the walk.
2. Select "show axes" to be see the axes, "fixed scale" to use a fixed scale when animating the walk and "colorize" (for moduli 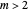 ) to display the walk using a rainbow color scheme, with the colors corresponding to the relative position along the walk.
) to display the walk using a rainbow color scheme, with the colors corresponding to the relative position along the walk.
3. Use the "number" setter bar to select from a variety of choices for the number  on which the walk is based.
on which the walk is based.
4. Check "show true random walk" to compare with a true random walk, constructed from a simulated sequence of independent Gauss–Kuzmin distributed digits). Select the "randomize" button to generate a new randomization of the true random walk.
5. Use the "modulus" setter bar to set the number of choices for each step in the walk.
References
[1] F. J. A. Artacho, D. H. Bailey, J. M. Borwein and P. B. Borwein, "Walking on Real Numbers," The Mathematical Intelligencer, 35(1), 2013 pp. 42–60. doi:10.1007/s00283-012-9340-x.
[2] J. Borwein, A. van der Poorten, J. Shallit and W. Zudilin, Neverending Fractions: An Introduction to Continued Fractions, Cambridge, UK: Cambridge University Press, 2014.
[3] A. Ya. Khinchin, Continued Fractions (translated from the Russian by Scripta Technica, Inc., English translation edited by H. Eagle.), 3rd ed., Chicago: University of Chicago Press, 1964.
Permanent Citation