Rational Roots of a Polynomial
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
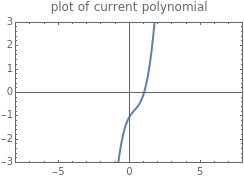
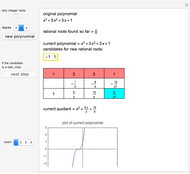
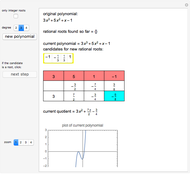
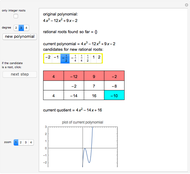
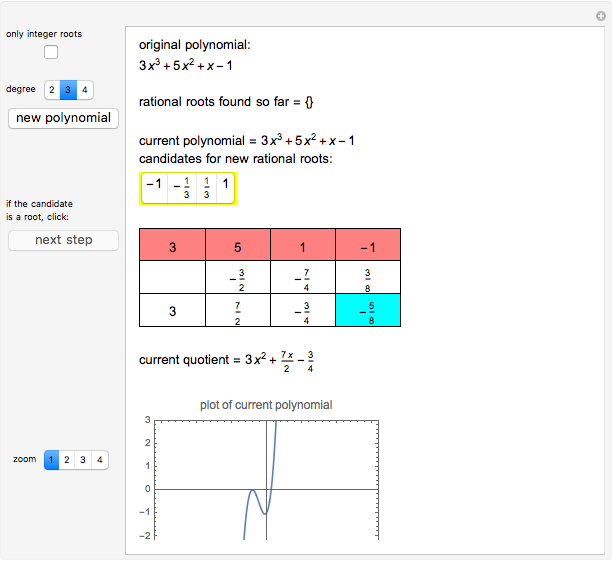
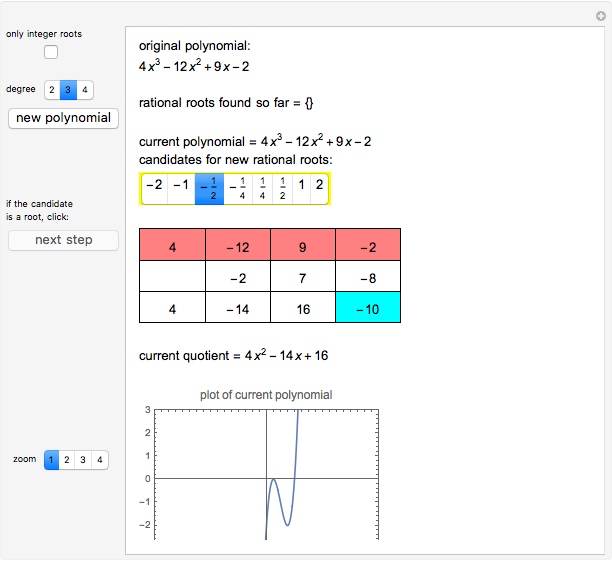
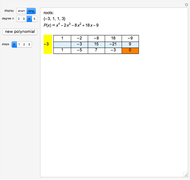
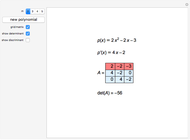
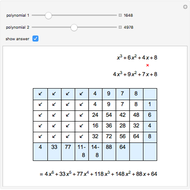
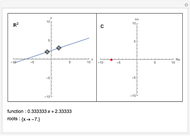
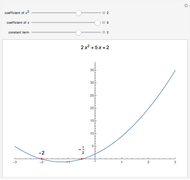
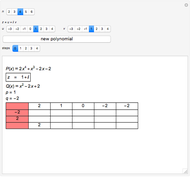
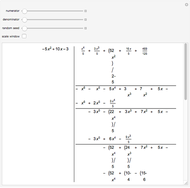
Let  be a polynomial with integer coefficients and constant coefficient
be a polynomial with integer coefficients and constant coefficient  . Use this Demonstration to find the rational roots of
. Use this Demonstration to find the rational roots of  .
.
Contributed by: Izidor Hafner (January 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation