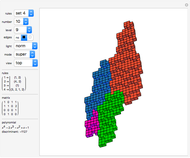
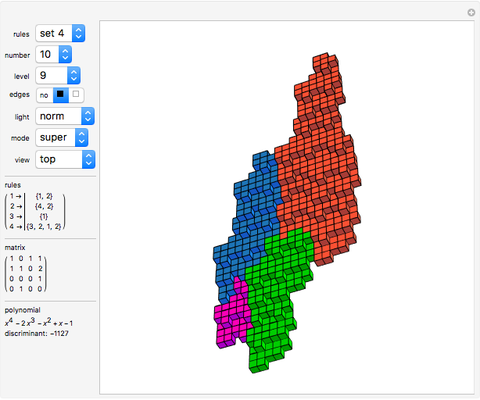
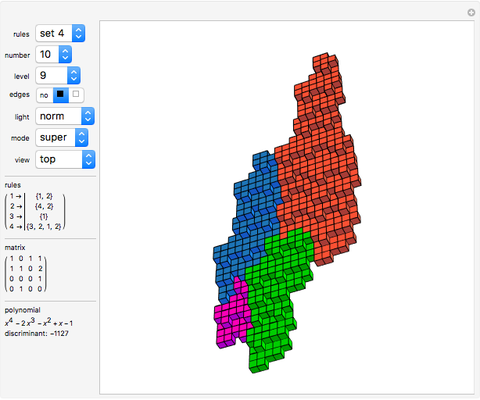
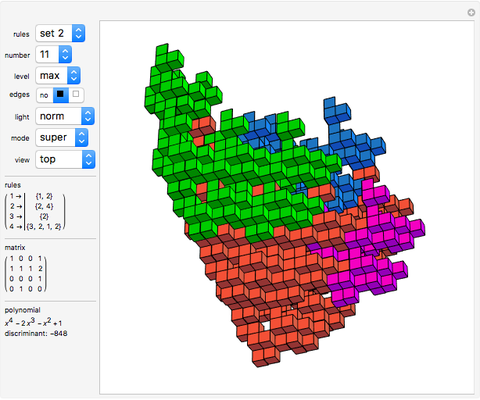
Rauzy Fractals of Order Four

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
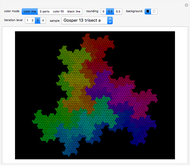
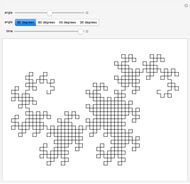
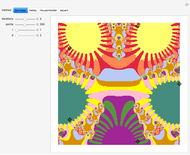
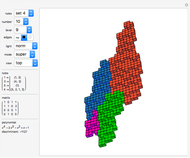
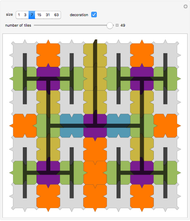
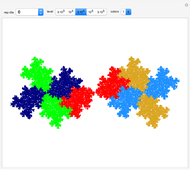
Experiment with 3D tilings based on unimodular Pisot substitutions of order four.
Contributed by: Dieter Steemann (April 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
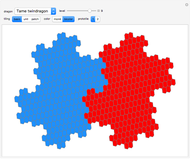
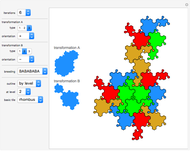
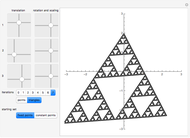
The common Rauzy fractal set is associated with the tribonacci substitution. Here the generation method based on a unimodular substitution of the Pisot type of order three (as demonstrated in [1]) is expanded to “tetrabonacci” substitutions of order four. An introduction to Pisot substitutions and Rauzy fractals is given by Arnoux and Ito [2]. Pisot means that the substitution has an incidence matrix with a unique eigenvalue of modulus greater than 1, and all other eigenvalues of modulus less than 1. Unimodular refers to a matrix with a determinant of  .
.
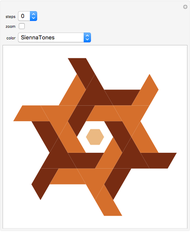
The core algorithms of this program follow the work of Barge and Kwapisz [3] expanded to order four. The tilings are defined by substitution rules using an alphabet of four letters,  in this case. The generated output is a 4D surface, where each letter of the substitution result corresponds to a specific 4D face. These faces are projected into the 3D space using the corresponding eigenvector of the Pisot eigenvalue. In the 3D space, every 4D face corresponds to a 3D prototile. This can be experienced by changing the 3D viewpoint or by manual rotation of the image result, best at low iteration levels and with colored edges. The given rules originate from our own experiments; they are different, but may include symmetries.
in this case. The generated output is a 4D surface, where each letter of the substitution result corresponds to a specific 4D face. These faces are projected into the 3D space using the corresponding eigenvector of the Pisot eigenvalue. In the 3D space, every 4D face corresponds to a 3D prototile. This can be experienced by changing the 3D viewpoint or by manual rotation of the image result, best at low iteration levels and with colored edges. The given rules originate from our own experiments; they are different, but may include symmetries.
Controls
rules: Use this popup menu in order to select a set of rules.
number: Use this popup menu to select a specific member of the current rule set.
level: Use this popup menu to set the iteration level. The level is limited so that the estimated number of tiles is less than 20,000. Level 0 shows the three prototiles; level 1 shows the initial arrangement of prototiles. "max" sets a level according to the estimated limit.
edges: Use this setter bar to select how the tile edges are depicted.
light: “norm” = normal (directional) lighting; “neutral” = white (undirected) ambient light.
mode: “super” tiles inherit color from their predecessor, so super tiles become visible. “proto” means colored according to the prototiles.
view: Use this popup menu to select a specific 3D viewpoint. Furthermore, you can rotate and pan the tile result in the output window by dragging it with the mouse.
Additional information about the selected rule is given by:
rules: Shows the replacement rule for each of the four tiles.
matrix/polynomial: The incidence matrix corresponding to the replacement rule, the characteristic polynomial of this matrix and the discriminant of the polynomial are displayed.
References
[1] D. Steemann, "Rauzy Fractals as Stepped Surfaces" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/RauzyFractalsAsSteppedSurfaces.
[2] P. Arnoux and S. Ito, "Pisot Substitutions and Rauzy Fractals," Bulletin of the Belgian Mathematical Society, 8, 2001 pp. 181–207. (Apr 13, 2018) iml.univ-mrs.fr/~arnoux/ArnouxIto.pdf.
[3] M. Barge and J. Kwapisz, "Geometric Theory of Unimodular Pisot Substitutions," American Journal of Mathematics, 128(5), 2006 pp. 1219–1282. www.jstor.org/stable/40068030.
Permanent Citation