Re-Orient a Sphere with Two Straight Rolls

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
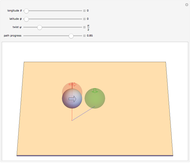
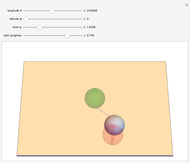
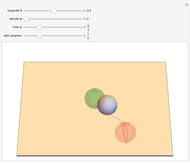
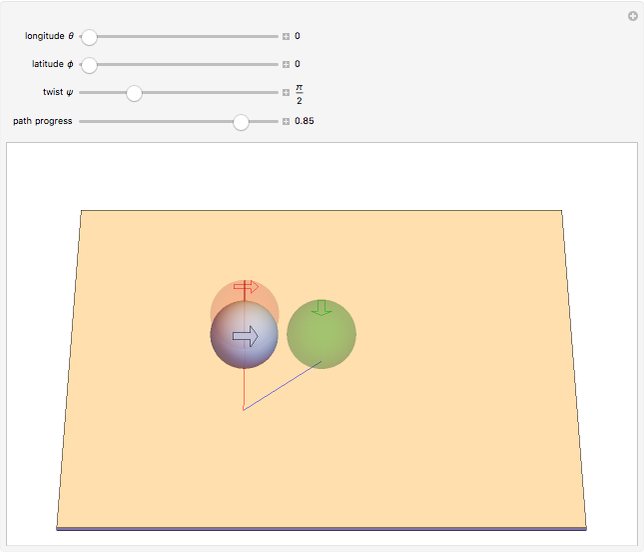
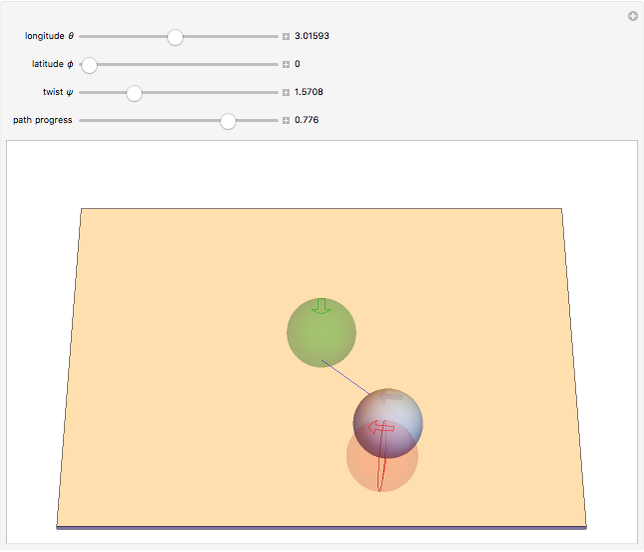
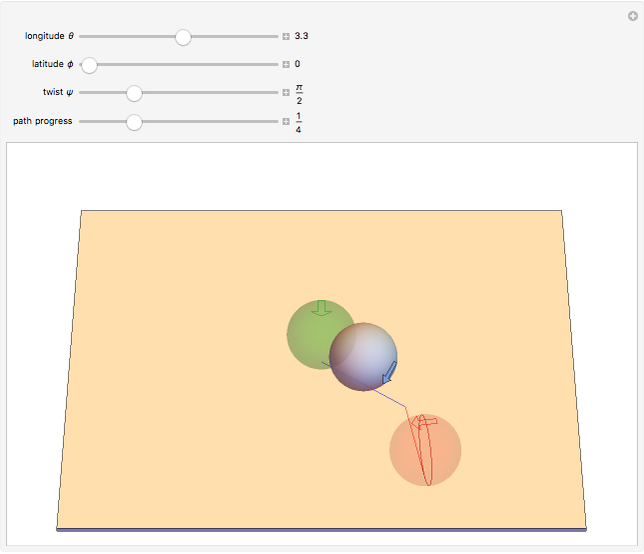
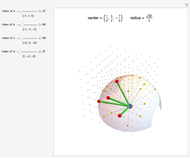
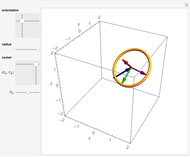
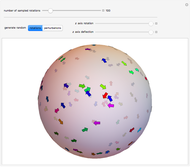
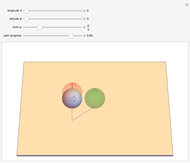
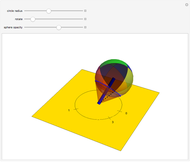
It is well-known that a sphere can be rolled in the horizontal plane to any orientation by three sequentially orthogonal rolls. This Demonstration shows that only two straight rolls are necessary. The desired orientation, shown in red, is specified by moving the north pole to a desired latitude  and longitude
and longitude  , then twisting about this pole by
, then twisting about this pole by 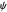 . Rolling from the initial orientation, shown in green, along the blue and red lines brings the sphere to the desired orientation.
. Rolling from the initial orientation, shown in green, along the blue and red lines brings the sphere to the desired orientation.
Contributed by: Aaron Becker (June 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The composite rotation of  about the
about the  axis,
axis,  about the
about the 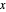 axis, and
axis, and  about the
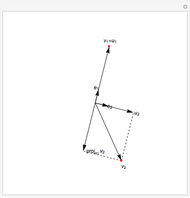
about the  axis can be reproduced by two straight rolls in the horizontal plane. For the unit sphere, a roll of
axis can be reproduced by two straight rolls in the horizontal plane. For the unit sphere, a roll of 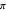 at an angle
at an angle 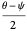 with the
with the 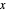 axis, followed by a roll of length
axis, followed by a roll of length 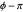 at an angle
at an angle  with the
with the 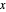 axis produces the same rotation.
axis produces the same rotation.
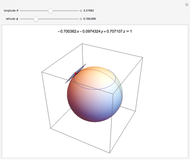
Any desired rotation can be specified by three sequentially orthogonal rotations:
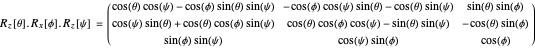
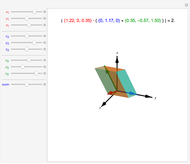
A rotation on the plane of length  , making angle
, making angle 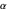 with the
with the 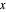 axis produces the rotation
axis produces the rotation

The two straight rolls 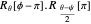 reproduce the desired rotation:
reproduce the desired rotation:
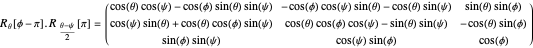
reference
[1] J. M. Hammersley, "7. Oxford Commemoration Ball," in Probability, Statistics and Analysis: London Mathematical Society Lecture Note Series, Number 79, ed. J. F. C. Kingman and G. E. H. Reuter, Cambridge University Press, 1983.
Permanent Citation