Reactor Design Economics
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
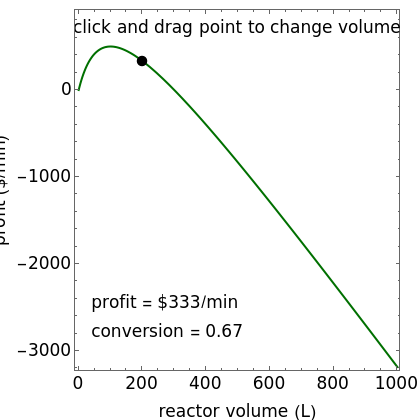
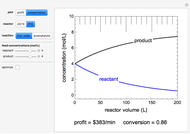
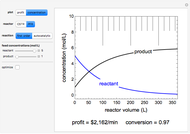
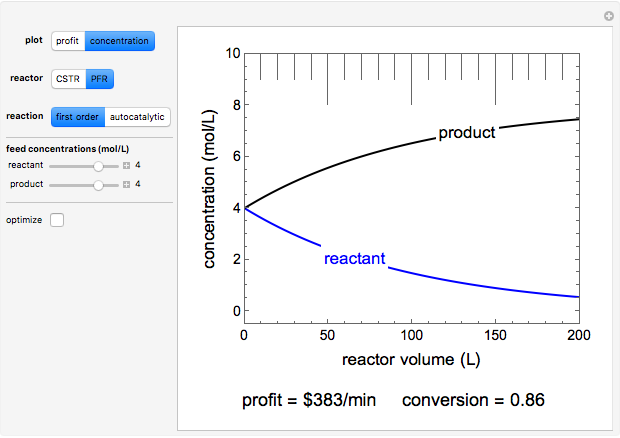
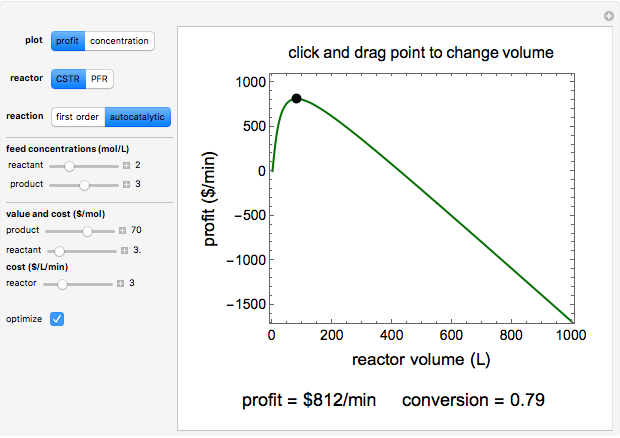
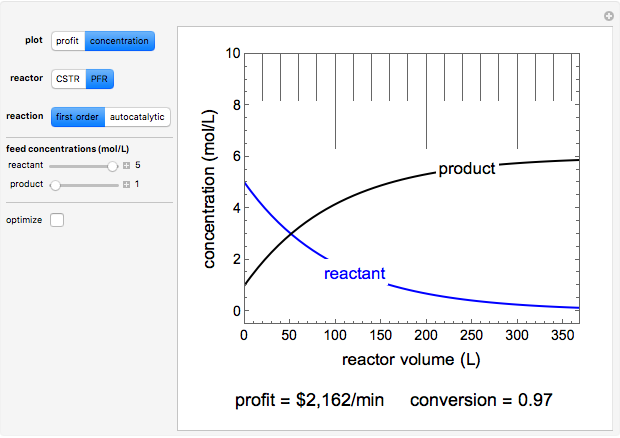
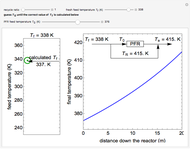
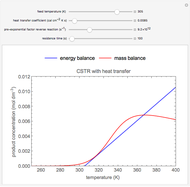
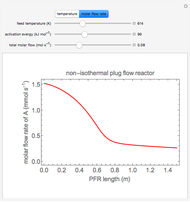
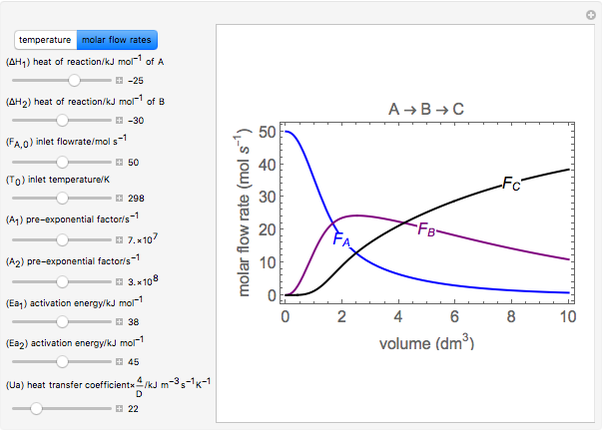
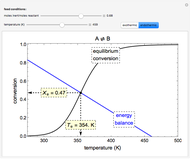
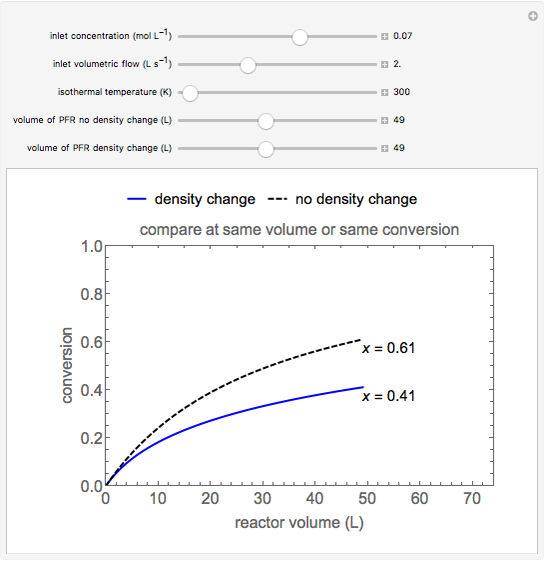
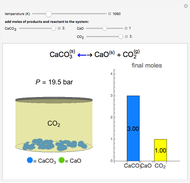
This Demonstration calculates the monetary profit as a function of reactor volume for a continuous stirred-tank reactor (CSTR) or a plug-flow reactor (PFR). The reaction is either first-order or autocatalytic; set the feed concentrations of reactant and product with sliders. Use sliders to set the value of the product and the costs of the reactant and reactor. Select "concentration" to view the reactant and product concentrations plotted versus reactor volume. The final volume corresponds to the volume at the black dot on the profit plot. Click and drag the black dot on the profit versus reactor volume plot. Check "optimize" to solve for the reactor volume with the highest profit. The separations cost is not considered in this Demonstration, but it can significantly affect profit.
Contributed by: Rachael L. Baumann and Garrison J. Vigil (November 2015)
Additional contributions by: John L. Falconer, Nathan S. Nelson, and Nick Bongiardina
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The rate of reaction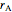 
for a first-order reaction 
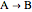is given by:
,
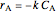and for an autocatalytic reaction it is:
,
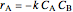where 
is the rate constant (1/min), and 
and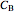 
are the reactant and product concentrations (mol/L).
A mass balance determines and 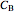for a continuous stirred-tank reactor (CSTR):
,
,
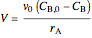where 
is the reactor volume (L),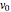 
is the inlet volumetric flow rate (L/s) and 
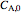and 
are the reactant and product feed concentrations (mol/L).
For a plug-flow reactor (PFR):
,
.
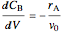Overall conversion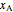 
of reactant 
to product and profit made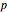 
are calculated:
;
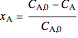for a CSTR:
,
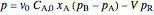for a PFR:
,
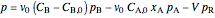where 
($/mol) and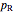 
($/[L min]) are the costs of the reactant and reactor and 
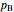($/mol) is the value of the product.
Permanent Citation
Continuous Stirred-Tank Reactor That Loses Cooling
Rachael L. Baumann
Isothermal Plug Flow Reactor with Recycle
Rachael L. Baumann
Multiple States in an Isothermal Continuous Stirred-Tank Reactor
Rachael L. Baumann
Adiabatic Plug Flow Reactor with Recycle
Rachael L. Baumann
Multiple Steady States in a Continuously Stirred Tank Reactor
Rachael L. Baumann
Parametric Sensitivity of Plug Flow Reactor With Heat Exchange
Rachael L. Baumann
Sensitivity of a Plug Flow Reactor to Model Parameters
Rachael L. Baumann
Reversible Reaction in an Adiabatic Plug-Flow Reactor
Rachael L. Baumann
Why Density Change Cannot Be Ignored in a Plug Flow Reactor (PFR)
Rachael L. Baumann
Reactor Rate and Conversion versus Space Velocity
Derek M. Machalek
