Reconstructing a Sampled Signal Using Interpolation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
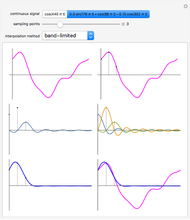
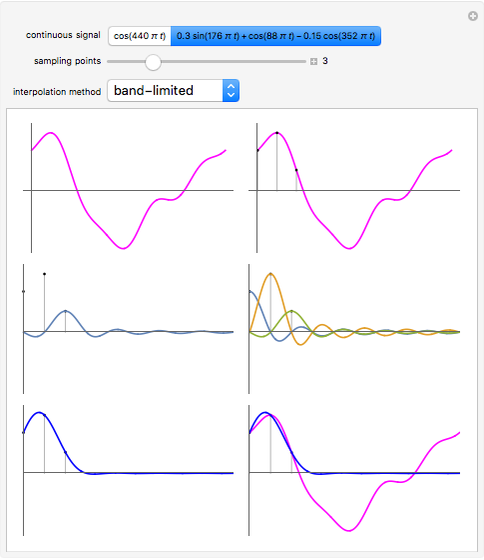
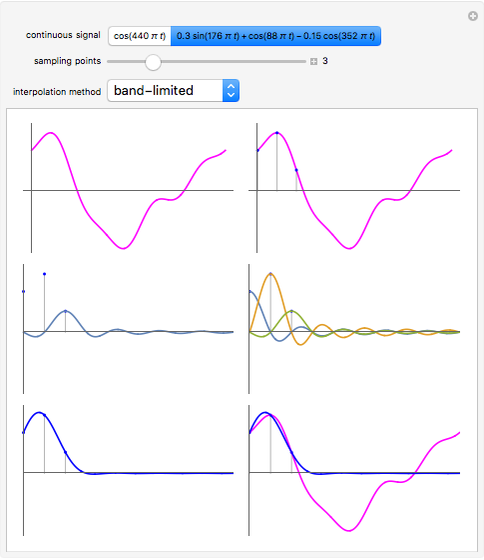
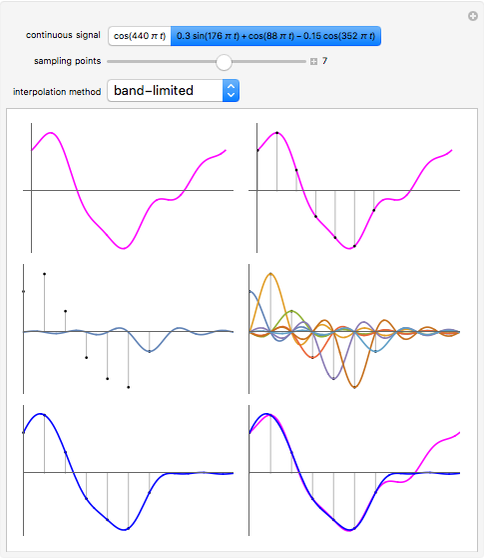
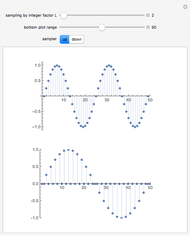
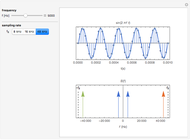
If a continuous signal  is sampled with a sampling period
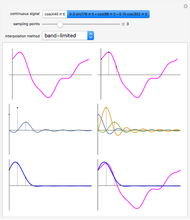
is sampled with a sampling period  then how can you approximately reconstruct the original signal? Three methods that are in use are zero-order hold interpolation, first-order hold interpolation, and band-limited interpolation. The reconstructed signal is calculated using
then how can you approximately reconstruct the original signal? Three methods that are in use are zero-order hold interpolation, first-order hold interpolation, and band-limited interpolation. The reconstructed signal is calculated using  , where
, where  is the value of the sample taken at time
is the value of the sample taken at time  and
and  is one of the three interpolation functions.
is one of the three interpolation functions.
Contributed by: David Bremner and Bruce Atwood (April 2011)
(Beloit College)
Open content licensed under CC BY-NC-SA
Details
For zero-order hold interpolation  , where
, where  is the rectangle (or unit box) function, equal to 1 for
is the rectangle (or unit box) function, equal to 1 for  and 0 otherwise; for first-order hold interpolation
and 0 otherwise; for first-order hold interpolation  , where
, where  is the unit triangle function on the interval
is the unit triangle function on the interval  ; and for band-limited interpolation
; and for band-limited interpolation  , where
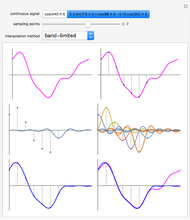
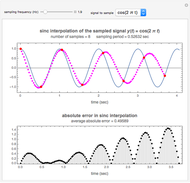
, where  . For these examples band-limited (sinc) interpolation gives the best results. This is not a surprise since the sampling theorem says a band-limited signal sampled at a frequency at least twice the highest frequency in the signal can be perfectly reconstructed from its samples using sinc interpolation if the summation is taken from
. For these examples band-limited (sinc) interpolation gives the best results. This is not a surprise since the sampling theorem says a band-limited signal sampled at a frequency at least twice the highest frequency in the signal can be perfectly reconstructed from its samples using sinc interpolation if the summation is taken from  to
to  .
.
For additional information see the lecture on interpolation by Prof. Alan V. Oppenheim at http://ocw.mit.edu/resources/res-6-007-signals-and-systems-spring-2011/video-lectures/lecture-17-interpolation.
Snapshots
Permanent Citation