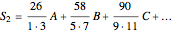Reconstruction of Vega's First Calculation of Pi

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
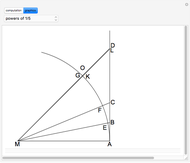
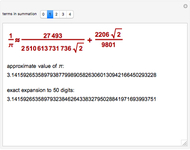
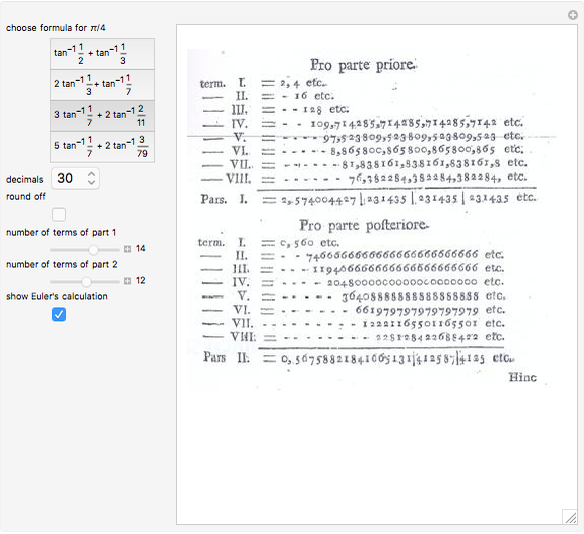
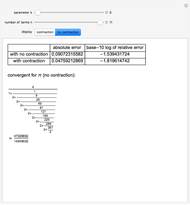
In 1789, Vega sent his first calculation of  to the Petersburg Academy. He used the formula
to the Petersburg Academy. He used the formula  , where
, where  is the smaller part and
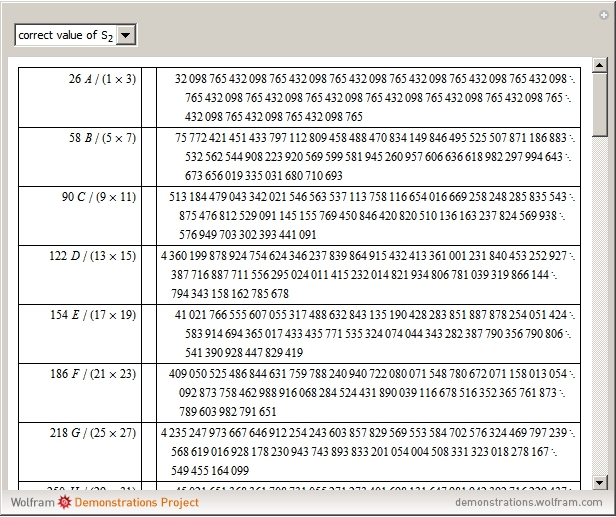
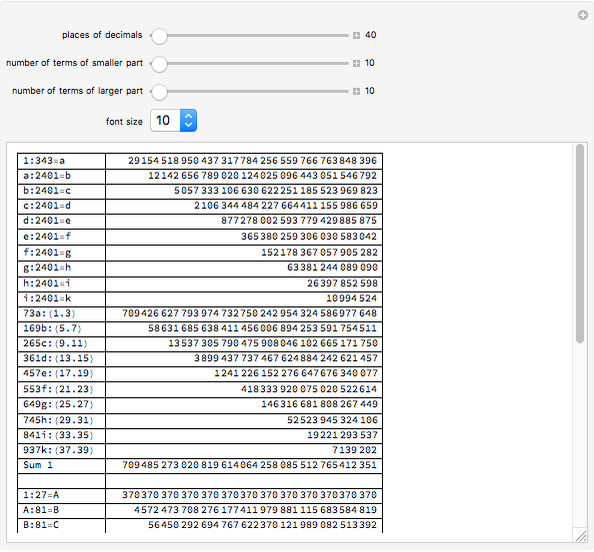
is the smaller part and  is the larger part. Vega calculated arctan by combining each positive term with the negative term following it. In this way, he got two series:
is the larger part. Vega calculated arctan by combining each positive term with the negative term following it. In this way, he got two series:
Contributed by: Izidor Hafner (November 2013)
Open content licensed under CC BY-NC-SA
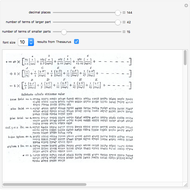
Snapshots
Details
References
[1] G. Vega, "Détermination de la circonférence d'un cercle," Nova Acta Academiae Scientiarum Imperialis Petropolitanae, IX, 1795 p. 41.
[2] W. W. R. Ball and H. S. M. Coxeter, Mathematical Recreations and Essays, 13th ed., New York: Dover, 1987 pp. 356–357.
[3] The MacTutor History of Mathematics Archive. "Georg Freiherr von Vega." (Jan, 2012) www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Vega.html.
Permanent Citation