Reed-Frost SEIR Model

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
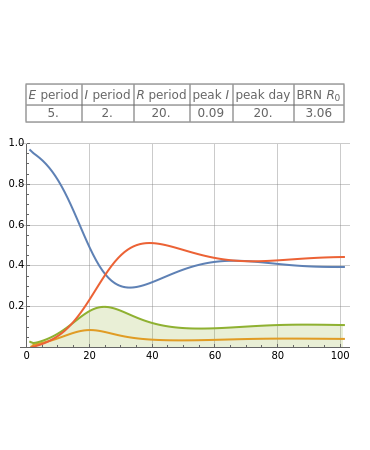
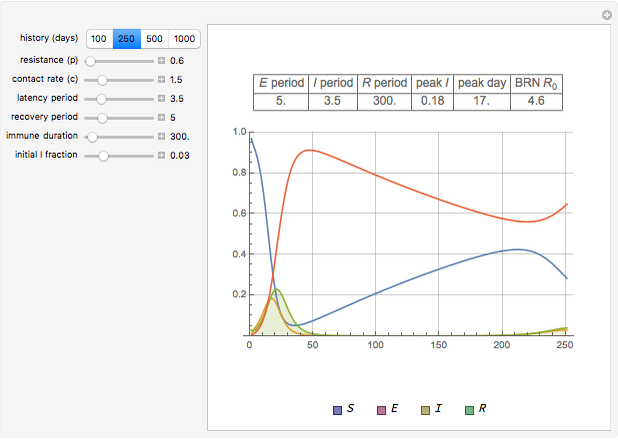
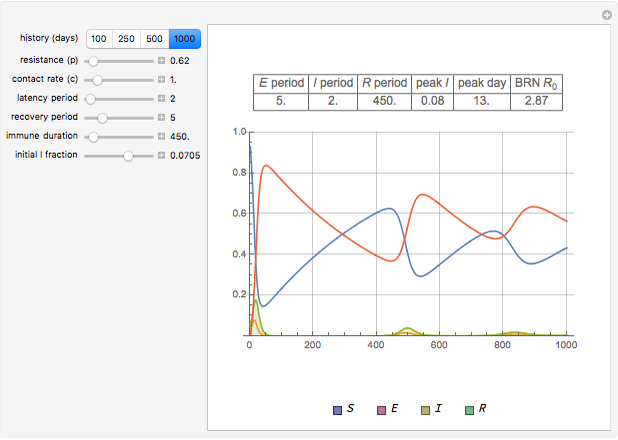
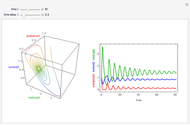
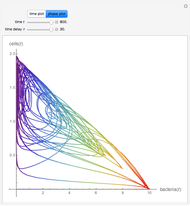
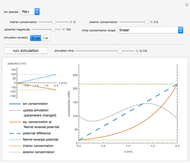
The Reed–Frost model for infection transmission is a discrete time-step version of a standard SIR/SEIR system: Susceptible, Exposed, Infectious, Recovered prevalences ( is blue,
is blue,  is purple,
is purple,  is olive/shaded,
is olive/shaded,  is green). This Demonstration lets you explore infection history for different choices of parameters, duration periods, and initial
is green). This Demonstration lets you explore infection history for different choices of parameters, duration periods, and initial  fraction.
fraction.
Contributed by: David Gurarie (May 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reed–Frost SIR/SEIR are discrete-time versions of infection transmission in a host population with standard (Susceptible, Exposed, Infectious, Recovered) compartments with the usual transition patterns:  .
.
The transition rate from each strata to the next is determined by a survival probability per unit time step (e.g. day). It measures what fraction of a given compartment will stay within the compartment. For instance, the fraction  of latent group
of latent group  would remain latent over one time step, while the complementary
would remain latent over one time step, while the complementary  would advance to the next level
would advance to the next level  . The force of infection
. The force of infection  depends on the resistance level of the
depends on the resistance level of the  group (probability to survive an infectious contact)
group (probability to survive an infectious contact)  , the contact rate
, the contact rate  (per day), and the infected population fraction
(per day), and the infected population fraction  (the product
(the product  gives the average number of infective contacts per day). Model parameters include:
gives the average number of infective contacts per day). Model parameters include:

The basic reproduction number (BRN) is  , which determines whether an infection outbreak occurs
, which determines whether an infection outbreak occurs  or dies out
or dies out  . It also controls the endemic level (provided
. It also controls the endemic level (provided  . In our setup, the total population
. In our setup, the total population 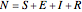 stays constant and the variables
stays constant and the variables  represent population fractions (or prevalences) relative to
represent population fractions (or prevalences) relative to  .
.
References
[1] Ohio Supercomputer Center Summer Institute. "Reed–Frost Epidemic Model." (May 22, 2012).
[2] Animal Population Health Institute, Colorado State University. "Deterministic and Stochastic Reed–Frost Epidemic Modeling Software." (May 22, 2012) http://reed-frostepi.sourceforge.net/index.php.
[3] G. Davis. "Simple Reed–Frost Equation." (May 22, 2012).
Permanent Citation