Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Reflective Properties of Conic Sections

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

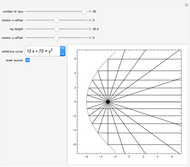
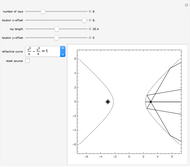
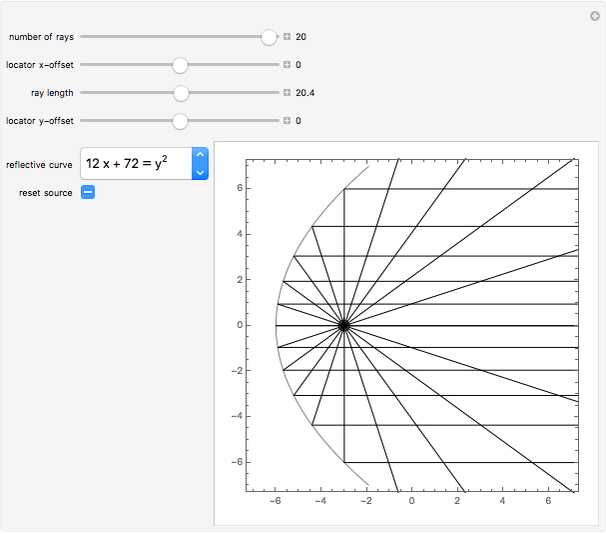
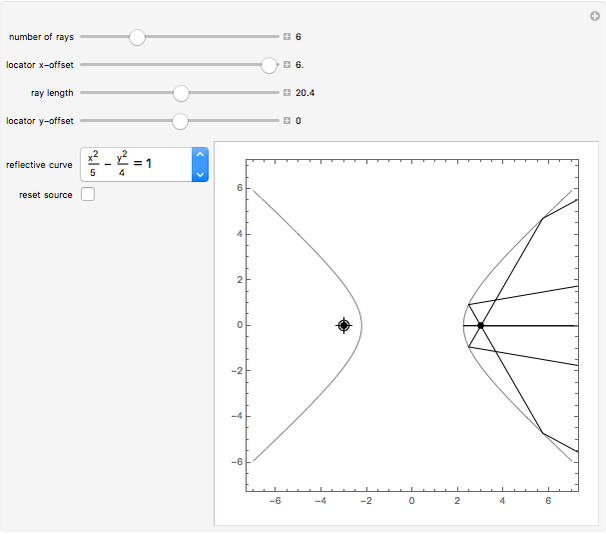
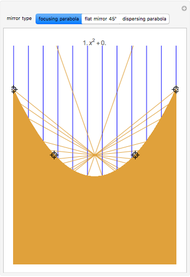
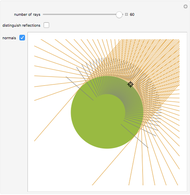
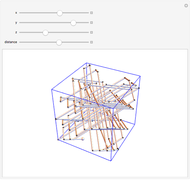
Conic sections, that is, ellipses, hyperbolas, and parabolas, all have special reflective properties. If the source of a signal is placed at one of the two focal points of an ellipse, the signal will be reflected to the other focal point. If the source is placed at one of the two focal points of a hyperbola, the signal will be reflected directly away from the other focal point. If the source is located at the one focus of a parabola, the signal will be reflected in lines parallel to the parabola's axis.

Contributed by: Robert Baker and Steven Wilkinson (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

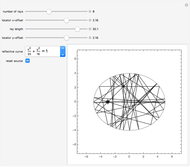
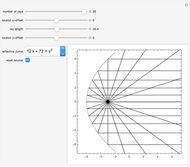
Choose one of five reflective curves. All but the last are conic sections; the last one will show no coherent reflective property, no matter where the source is placed.

Rays emanate from the source. Choose the desired number of equally spaced rays using the "number of rays" slider. Choose how long the signal is from the source using the "ray length" slider.

Choose the source of the signal by dragging the locator, or using the "locator -offset" and "locator -offset" sliders.

The source starts at one of the focal points for all the conic sections. If you move the source and want it returned to the original focus, click the "reset source" checkbox.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send