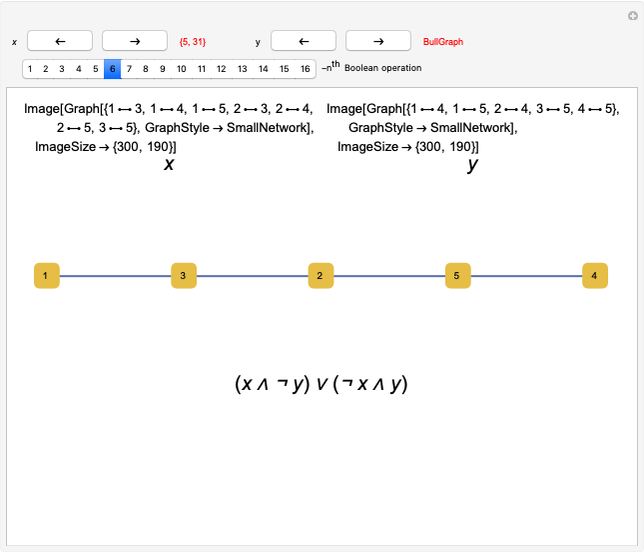
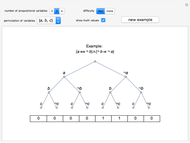
Representation of Three-Valued Boolean Functions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
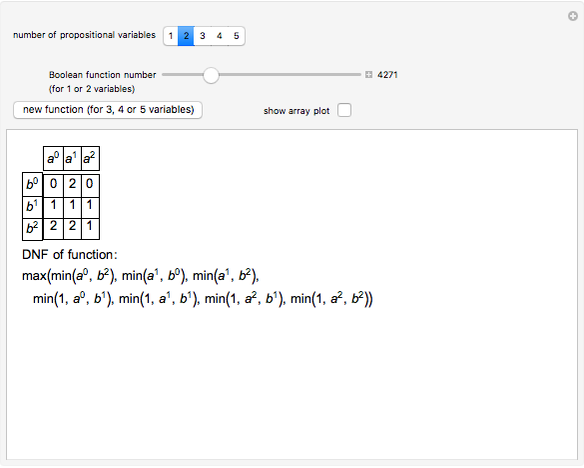
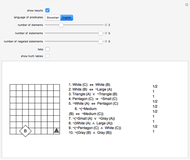
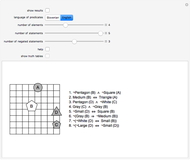
This Demonstration displays three-valued Boolean functions of  arguments. If
arguments. If  , the disjunctive normal form (DNF) of a function is also given. If
, the disjunctive normal form (DNF) of a function is also given. If  , a random function is given.
, a random function is given.
Contributed by: Izidor Hafner (September 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A three-valued logic function  of
of  arguments is represented by
arguments is represented by  . There are
. There are  such functions; if
such functions; if  , there are nine and if
, there are nine and if  , there are 19,683.
, there are 19,683.
The roles of conjunction and disjunction are played by the functions  and
and  .
.
Define three functions  for
for 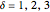 :
:
 if
if  and 0 otherwise.
and 0 otherwise.
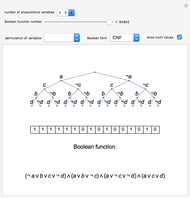
Each function of  arguments can be represented in disjunctive normal form (DNF):
arguments can be represented in disjunctive normal form (DNF):
 ,
,
where  and the maximum is taken over all
and the maximum is taken over all  tuples with components from
tuples with components from 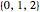 .
.
It follows that the constants 0, 1, 2 together with the functions  ,
,  and
and  form a basis for three-valued Boolean functions [2, pp. 245–246].
form a basis for three-valued Boolean functions [2, pp. 245–246].
In 1936, SŁupecki [1, pp. 335–337] showed that all three-valued functions could be defined using implication and negation from Łukasiewicz three-valued logic plus the constant function called "tertium",  1.
1.
In  -valued logic, the Sheffer–Webb function
-valued logic, the Sheffer–Webb function  (an analog of the Sheffer stroke function, NAND) forms a basis for
(an analog of the Sheffer stroke function, NAND) forms a basis for  -valued logic [2, p. 247].
-valued logic [2, p. 247].
References
[1] M. Gardner, Logic Machines, Diagrams and Boolean Algebra, New York: Dover Publications, 1968.
[2] S. G. Gindikin, Algebraic Logic in Problems (in Russian), Moscow: Nauka Publishers, 1972.
[3] J. SŁupecki, "The Full Three-Valued Propositional Calculus," Polish Logic 1920–1930, S. McCall (ed.), Oxford: Oxford University Press, 1967.
Permanent Citation