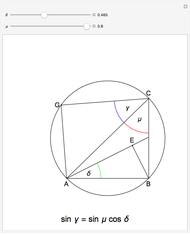
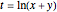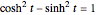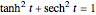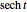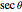Representations of Trigonometric and Hyperbolic Functions in Terms of Sector Areas

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
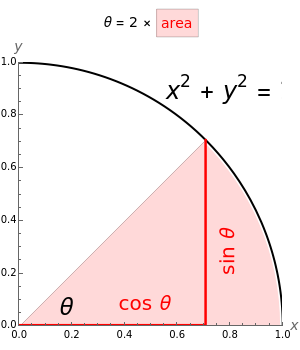
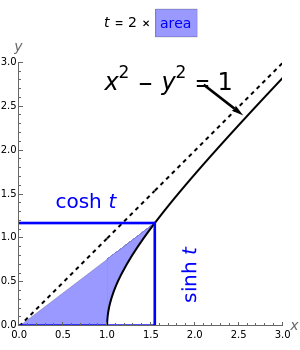
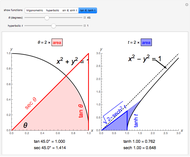
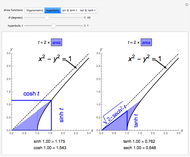
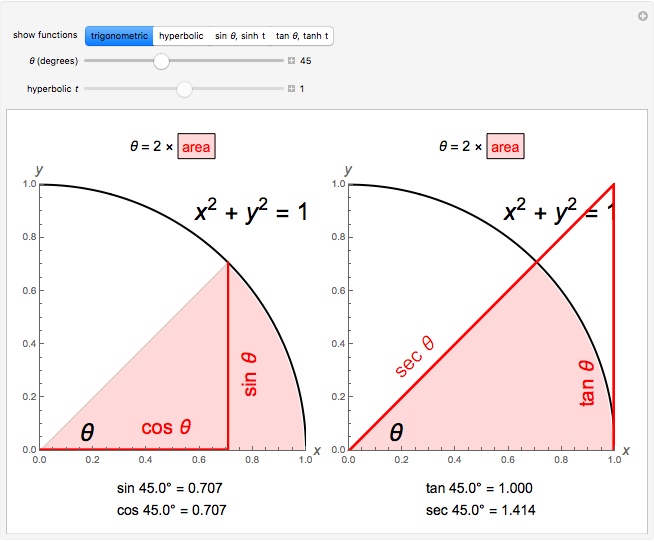
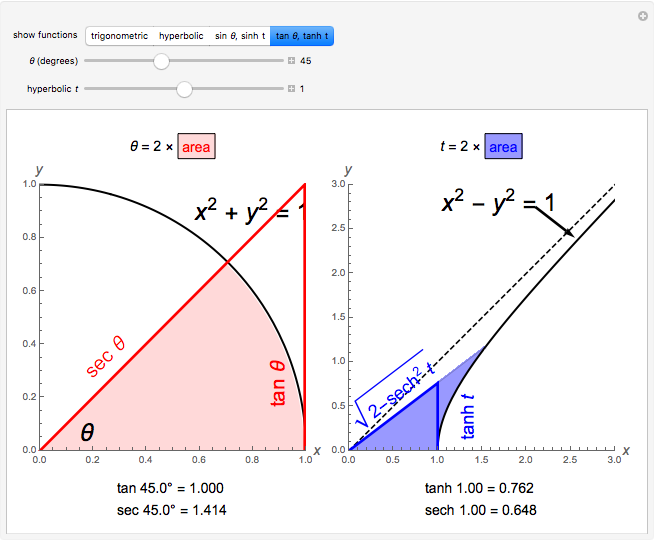
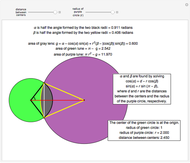
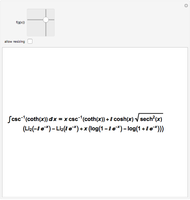
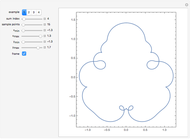
A sector of angle  of a unit circle
of a unit circle 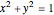 has an area equal to
has an area equal to 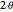 radians. So half the area can serve as the argument for the trigonometric functions via parametric equations for
radians. So half the area can serve as the argument for the trigonometric functions via parametric equations for  and
and  . The two constructions shown are consistent with the trigonometric identities
. The two constructions shown are consistent with the trigonometric identities  and
and 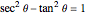 . (As a consequence, circular functions are alternatively called trigonometric functions.)
. (As a consequence, circular functions are alternatively called trigonometric functions.)
Contributed by: S. M. Blinder (August 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
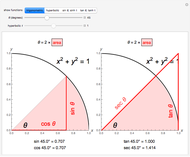
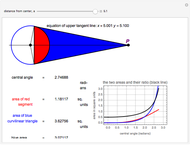
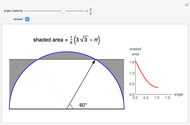
The thumbnail and the third snapshot show the comparative behavior of corresponding trigonometric and hyperbolic functions.
Reference
[1] S. M. Blinder, Guide to Essential Math, Amsterdam: Elsevier Academic Press, 2008, pp. 71–72, 188–189.
Permanent Citation