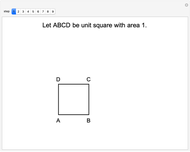
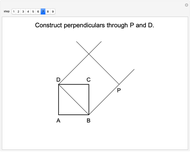
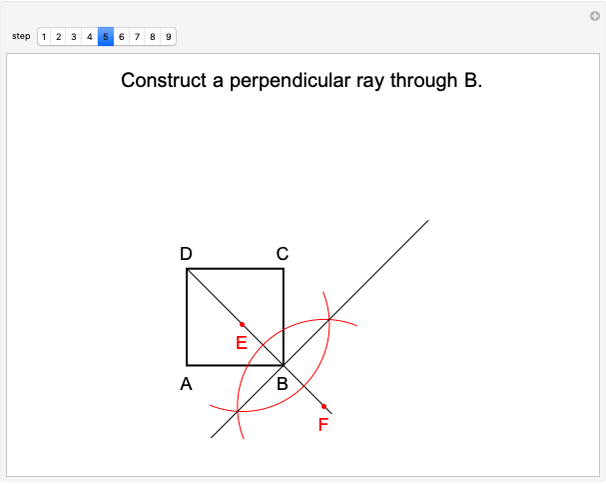
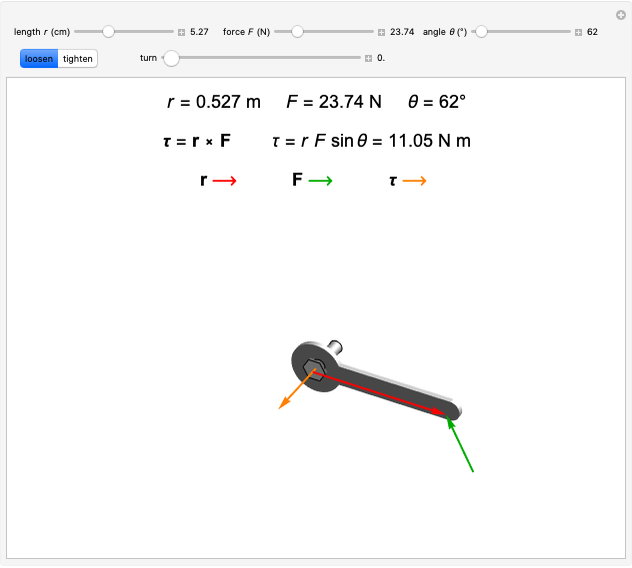
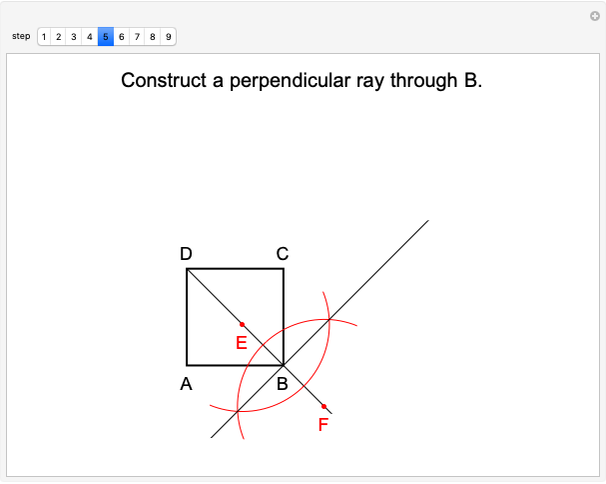
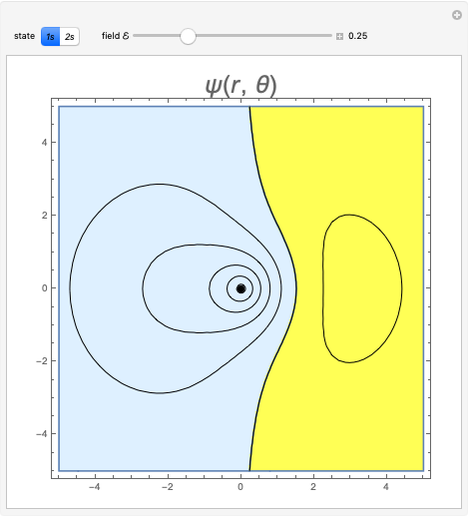
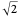Ruler and Compass Construction of a Square with Doubled Area

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
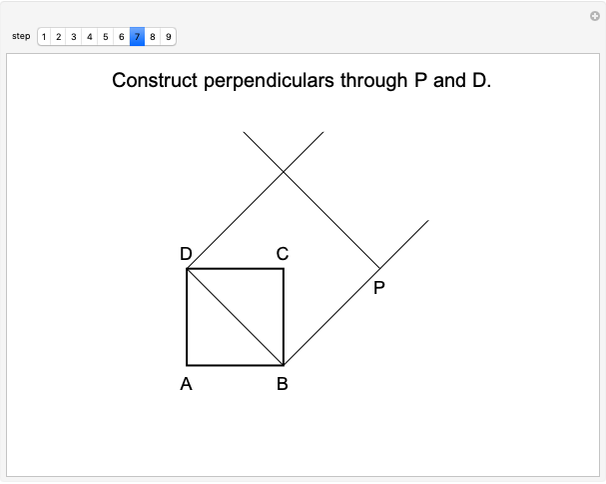
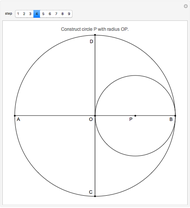
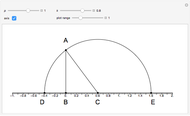
Mathematicians in ancient Greece showed that ruler and compass constructions could be used in a wide variety of geometrical operations. Some elementary examples are: drawing a line (or ray) through two points, drawing a circle (or arc) of arbitrary radius centered at a point, creating a point at the intersection of two nonparallel lines and drawing a perpendicular to a line at a given point. Three geometric constructions sought from antiquity are squaring a circle, doubling a cube and trisecting an arbitrary angle. These have since been shown to be impossible using only a ruler and compass.
[more]
Contributed by: S. M. Blinder (August 2022)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] K. Brakke. "Ruler and Compass Construction Doubling the Area of a Given Square." (Sep 30, 2021) facstaff.susqu.edu/brakke/rulerandcompass/20-doubledsquare.html.
Permanent Citation