SEIRD Model for Analyzing Coronavirus (COVID-19) Pandemic

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
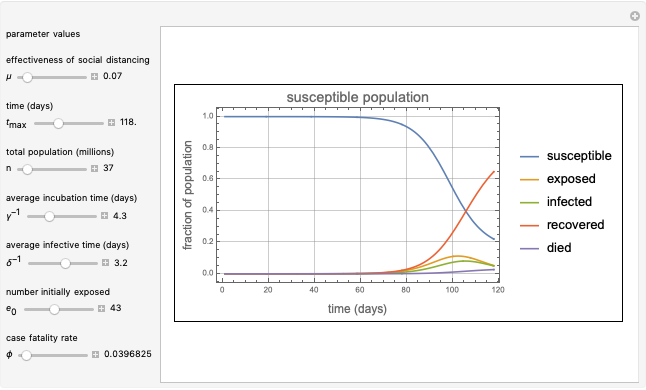
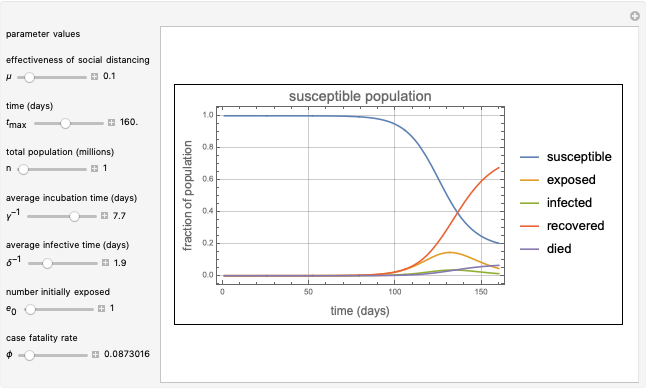
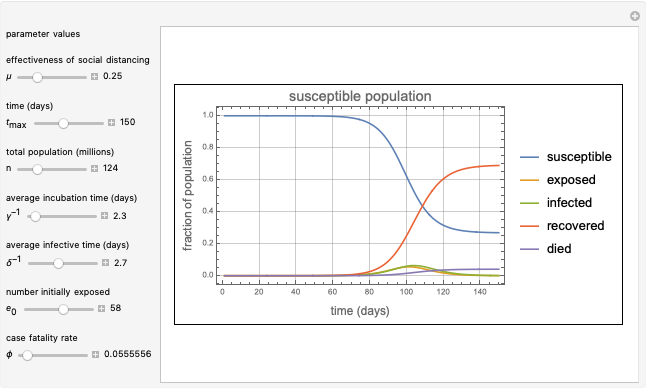
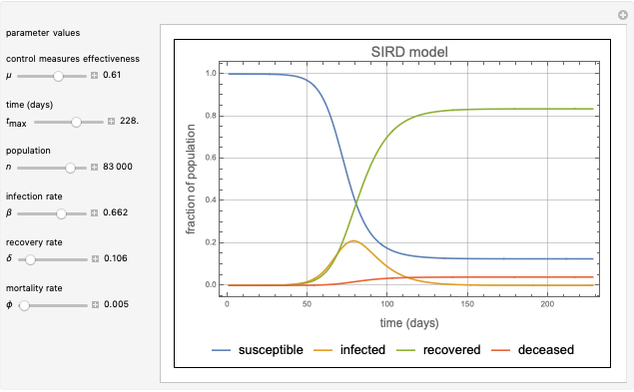
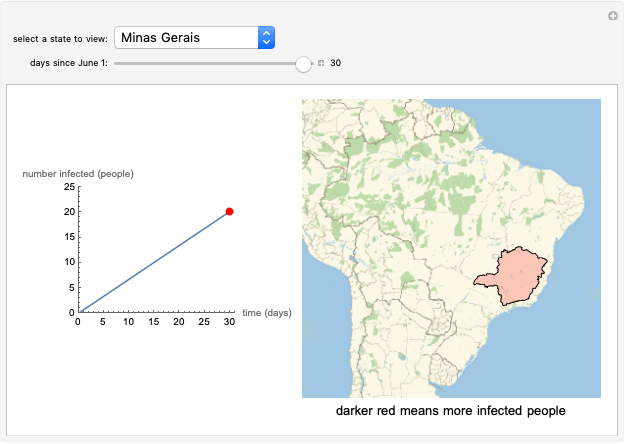
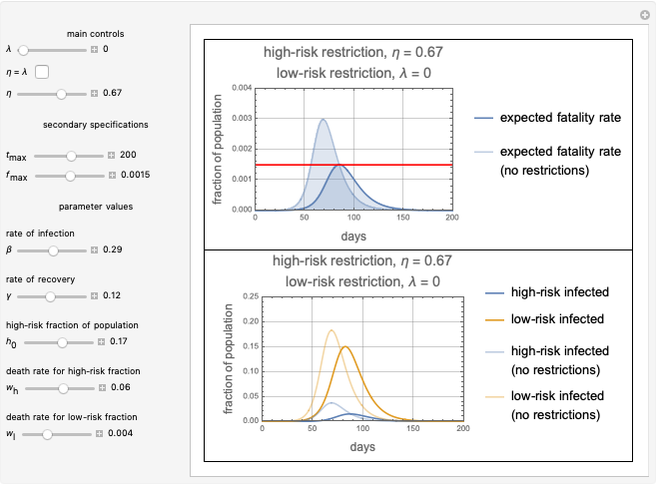
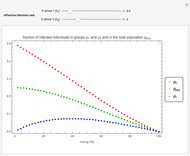
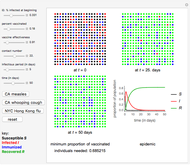
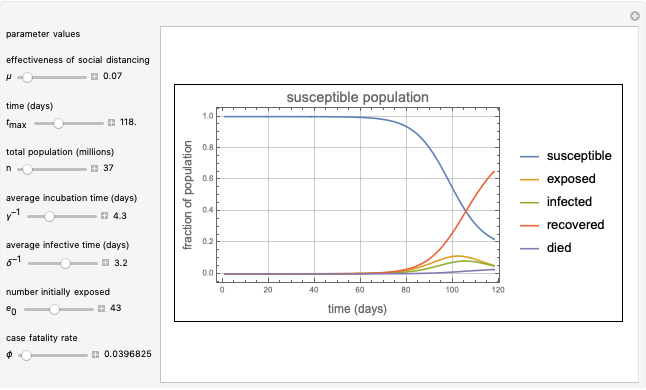
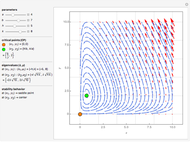
This Demonstration presents a susceptible\[Hyphen]exposed\[Hyphen]infectious\[Hyphen]recovered-died (SEIRD) model for analyzing the coronavirus (COVID-19) pandemic. A control parameter  with a value in the range
with a value in the range 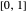 is introduced into the model to measure the effectiveness of a social distancing policy. The higher the value of
is introduced into the model to measure the effectiveness of a social distancing policy. The higher the value of  , the more effective the control policy. The parameters of the model were obtained by using the vast data provided about the pandemic on a daily basis by several scientific organizations. The model makes predictions on the turning points and possible vanishing time of the pandemic for a given population and initial number of exposed persons.
, the more effective the control policy. The parameters of the model were obtained by using the vast data provided about the pandemic on a daily basis by several scientific organizations. The model makes predictions on the turning points and possible vanishing time of the pandemic for a given population and initial number of exposed persons.
Contributed by: Wusu Ashiribo Senapon and Olabanjo Olusola Aanu (April 2020)
(Department of Mathematics and Department of Computer Science, Lagos State University, Lagos, Nigeria)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The SEIRD model for COVID-19 implemented in this Demonstration is the coupled system of ordinary differential equations:
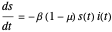 ,
,
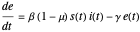 ,
,
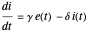 ,
,
 ,
,
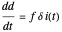 ,
,
where
 = susceptible fraction of the population,
= susceptible fraction of the population,
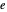 = exposed fraction of the population,
= exposed fraction of the population,
 = infected fraction of the population,
= infected fraction of the population,
 = fraction of population that has recovered,
= fraction of population that has recovered,
 = fraction of population that has died of the infection,
= fraction of population that has died of the infection,
 = effectiveness of control (social distancing) measure,
= effectiveness of control (social distancing) measure,
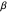 = infection rate,
= infection rate,
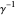 = average incubation time (days),
= average incubation time (days),
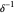 = average infective time (days),
= average infective time (days),
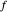 = case fatality rate.
= case fatality rate.
References
[1] Nigeria Centre for Disease Control.
[2] World Health Organization. "Coronavirus Disease 2019 (COVID-19) Situation Report–74." (Apr 22, 2020) www.who.int/docs/default-source/coronaviruse/situation-reports/20200403-sitrep-74-covid-19-mp.pdf?sfvrsn=4e043d03_12.
[3] Worldometer. "COVID-19 Coronavirus Pandemic." (Apr 22, 2020) www.worldometers.info/coronavirus.
[4] L. Peng, W. Yang, D. Zhang, C. Zhuge and L. Hong, "Epidemic Analysis of COVID-19 in China by Dynamical Modeling," medRxiv, 2020. doi:10.1101/2020.02.16.20023465.
[5] B. M. Ndiaye, L. Tendeng and D. F. Seck, "Analysis of the COVID-19 Pandemic by SIR Model and Machine Learning Technics for Forecasting." arxiv.org/abs/2004.01574v1.
Permanent Citation