Wolfram Demonstrations Project

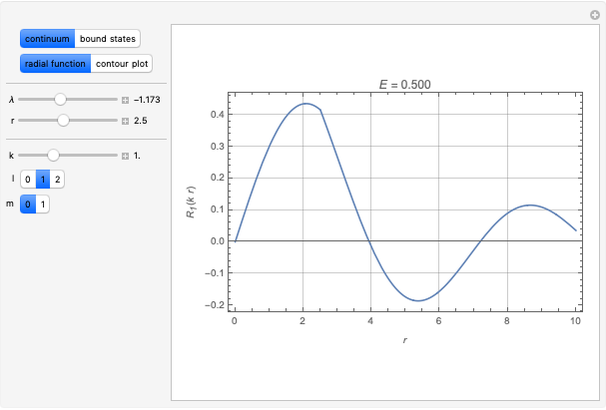
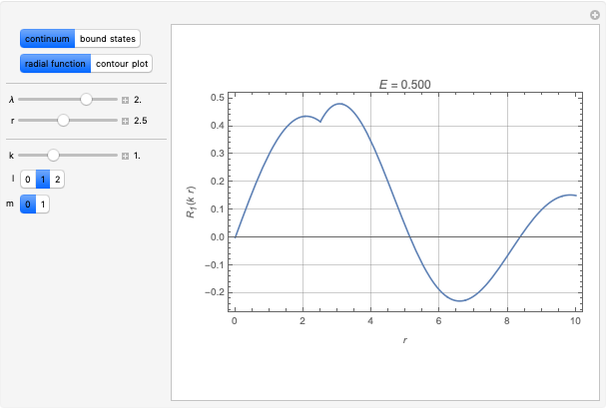
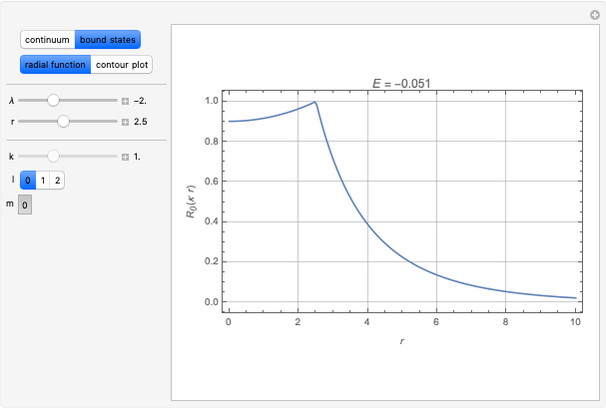
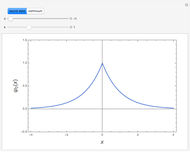
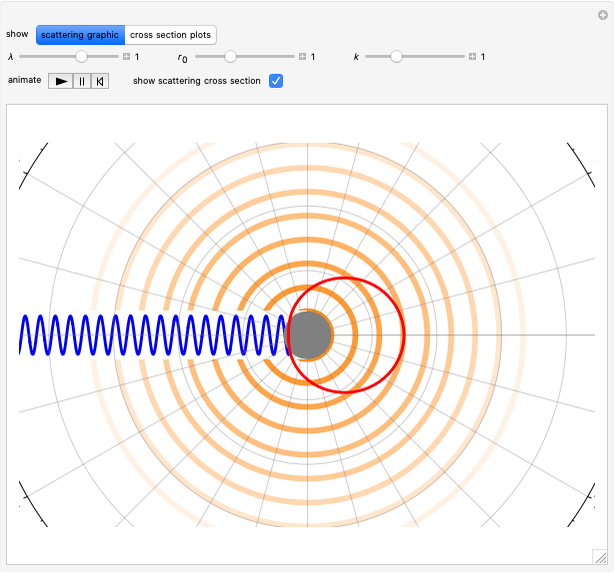
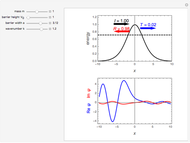
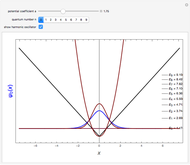
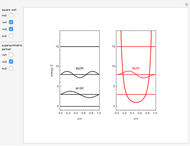
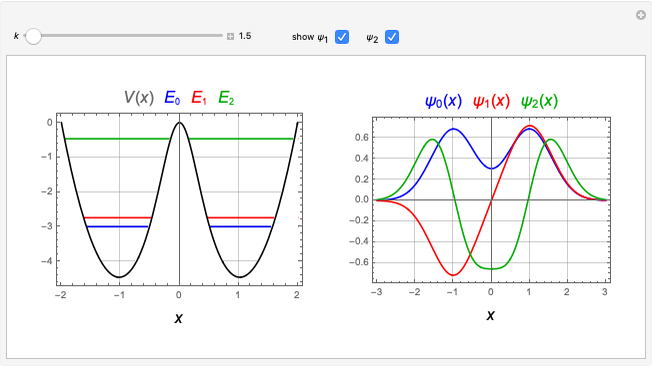
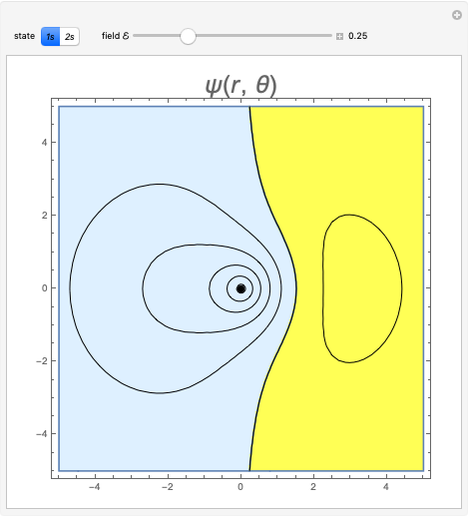
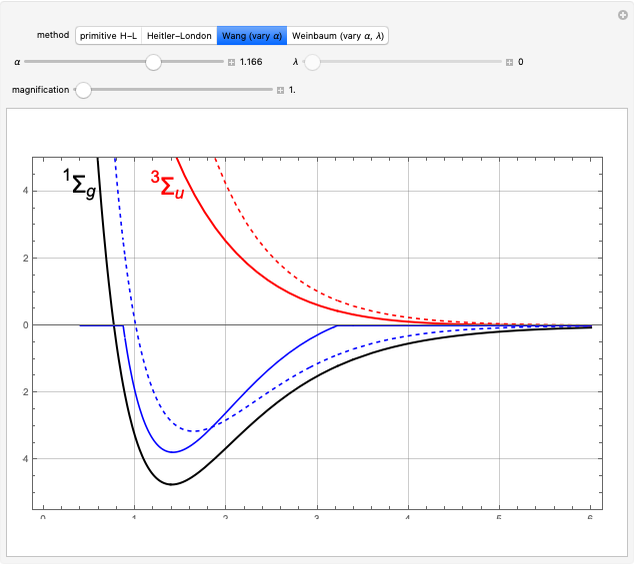
The Schrödinger equation has been solved in closed form for about 20 quantum-mechanical problems. This Demonstration describes one such example published some time ago. A particle moves in a potential that is zero everywhere except on a spherical bubble of radius

, drawn as a red circle in the contour plots. This result has been applied to model the buckminsterfullerene molecule

and also to approximate the interatomic potential in the helium van der Waals dimer

The relevant Schrödinger equation is given by

, in units with

and

in bohrs, and

in hartrees. For

, the equation has separable continuum solutions

, where the

are spherical harmonics. The radial function has the form

for

and

for

. Here

and

are spherical Bessel functions and the

are phase shifts. For each value of

, a single bound state will exist, provided that

. If no bound state exists, the plot will remain blank. The bound-state radial function is

, where

and

are the greater and lesser of

and

, and

is a Hankel function. The energy is given by

, with

determined by the transcendental equation

. Both the bound and continuum wavefunctions are continuous at

but have discontinuous first derivatives. The second derivative produces a deltafunction.

This Demonstration shows plots of the radial functions

and a cross section of the density plots of

for

. The wavefunction is positive in the blue regions and negative in the white regions. Be cautioned that the density plots might take some time to complete.

Contributed by: S. M. Blinder

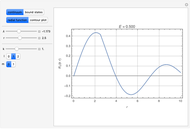
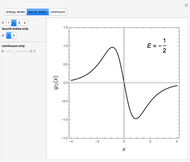
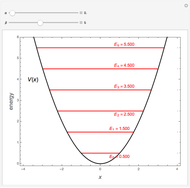
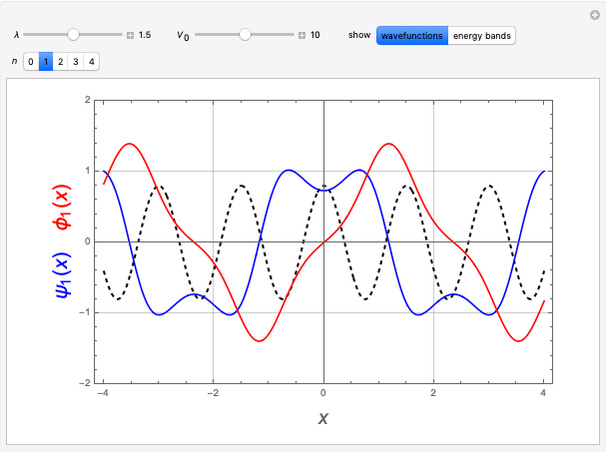
Snapshot 1: radial function of a continuum state

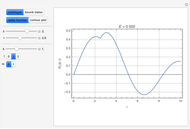
Snapshot 2: radial function for a bound state

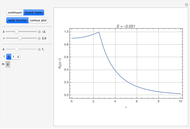
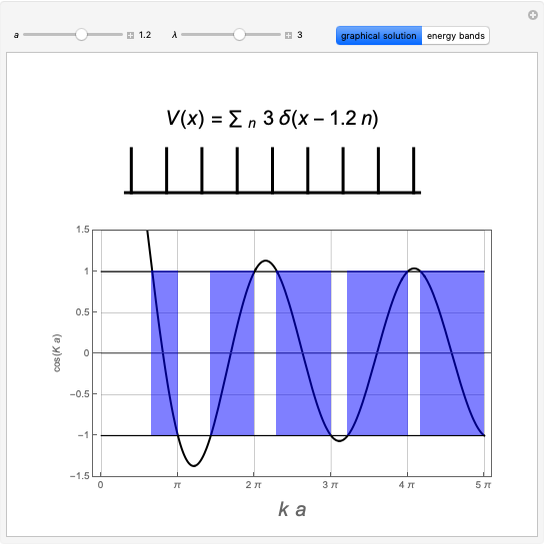
Snapshot 3: contour plot of a continuum

Reference

[1] S. M. Blinder, "Schrödinger Equation for a Dirac Bubble Potential," Chemical Physics Letters, 64(3), 1979 pp. 485–486. doi:10.1016/0009-2614(79)80227-4.