Sensitive Dependence on Initial Conditions in a Simple Three-Body Problem

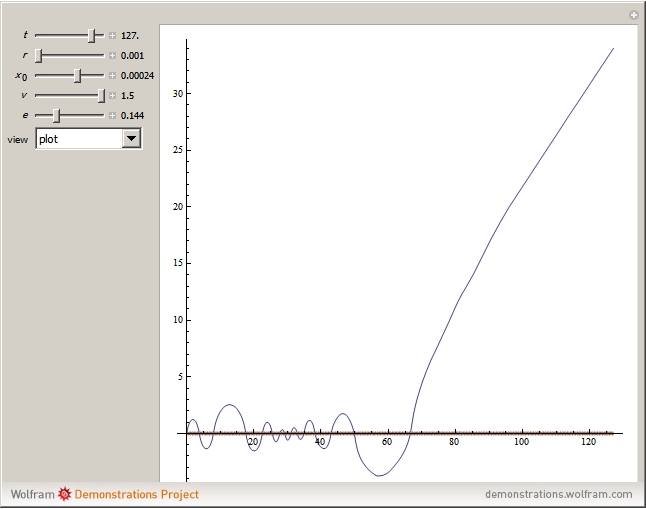
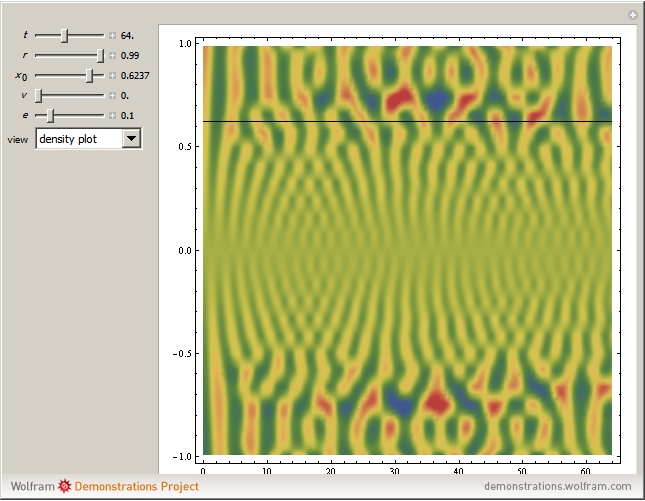
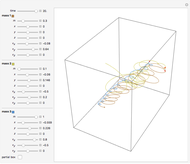
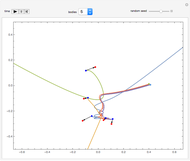
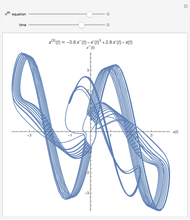
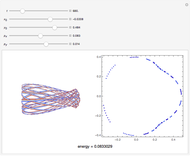
A planet moves under the gravitational influence of two stars of equal mass (very large compared with the planet), in orbits with eccentricity around their center of gravity. The planet moves in a plane perpendicular to the plane of the stars, passing through their center of gravity. The differential equation is solved for initial position in the range and velocity . The system shows sensitive dependence on initial conditions, despite the simplicity of the equation of motion. This problem was studied by the Soviet mathematician Kirill Sitnikov.