Simple Dynamics of Epidemics, the Reproduction Number

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
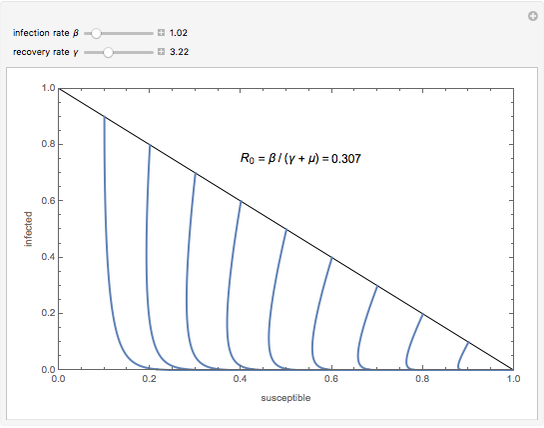
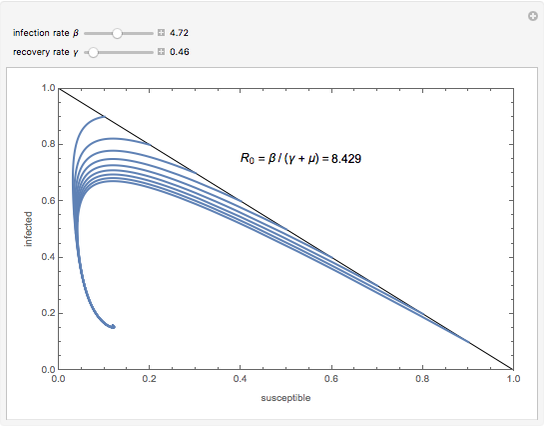
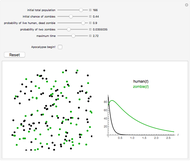
In epidemiology, the basic reproduction number  is the expected number of new infections from a single infection in a population where all subjects are susceptible [1]. This metric is useful because it helps determine whether or not an infectious disease can spread through a population. When
is the expected number of new infections from a single infection in a population where all subjects are susceptible [1]. This metric is useful because it helps determine whether or not an infectious disease can spread through a population. When  , the infection will die in the long run. But if
, the infection will die in the long run. But if  , the infection will spread in the population. Generally, the greater the value of
, the infection will spread in the population. Generally, the greater the value of  , the harder it is to control the epidemic. This Demonstration solves a simple epidemic model and shows the conditions necessary for the outbreak of an infection to result in an epidemic.
, the harder it is to control the epidemic. This Demonstration solves a simple epidemic model and shows the conditions necessary for the outbreak of an infection to result in an epidemic.
Contributed by: Clay Gruesbeck (December 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Consider an SIR model in which we divide the population into three parts: susceptible, infected, and recovered, in the proportions  ,
,  , and
, and  , so that
, so that  . Suppose the birth rate is a constant
. Suppose the birth rate is a constant  equal to the death rate. The model is:
equal to the death rate. The model is:
 ,
,
 ,
,
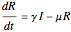 ,
,
where 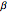 is the infection rate and
is the infection rate and  is the recovery rate, with the initial
is the recovery rate, with the initial  ,
,  , and
, and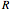 non-negative. There is an outbreak only if
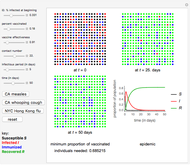
non-negative. There is an outbreak only if  , and the outbreak results in an epidemic only if
, and the outbreak results in an epidemic only if  ; otherwise the infection will die out [1].
; otherwise the infection will die out [1].
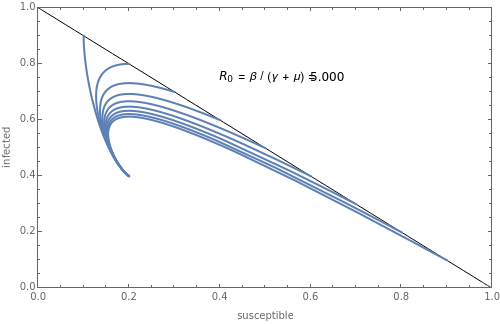
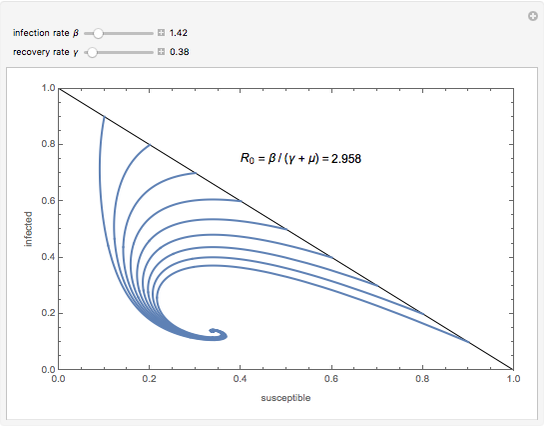
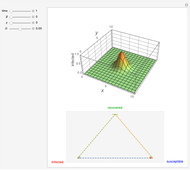
The SIR equations are solved and the result presented in a plot in the  -
- plane for various initial values of
plane for various initial values of  and
and  , with initial value
, with initial value  . You can vary the values of the infection rate
. You can vary the values of the infection rate 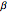 and the recovery rate
and the recovery rate  to follow the trajectory of the SIR system.
to follow the trajectory of the SIR system.
Reference
[1] Wikipedia. "Compartmental Models in Epidemiology." (Dec 14, 2012) en.wikipedia.org/wiki/Compartmental_models_in _epidemiology.
Permanent Citation