Simplified Hartree-Fock Computations on Second-Row Atoms

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
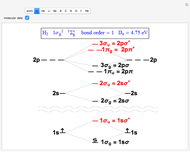
Modern computational quantum chemistry has developed largely from applications of the Hartree–Fock method to atoms and molecules [1–3]. A simple representation of a many-electron atom is given by a Slater determinant constructed from  occupied spin-orbitals:
occupied spin-orbitals:
Contributed by: S. M. Blinder (October 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
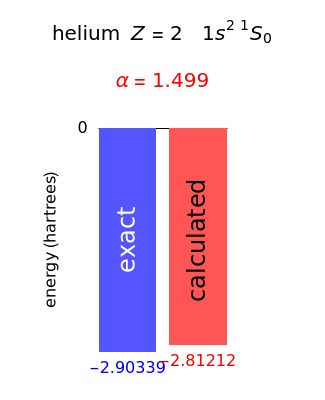
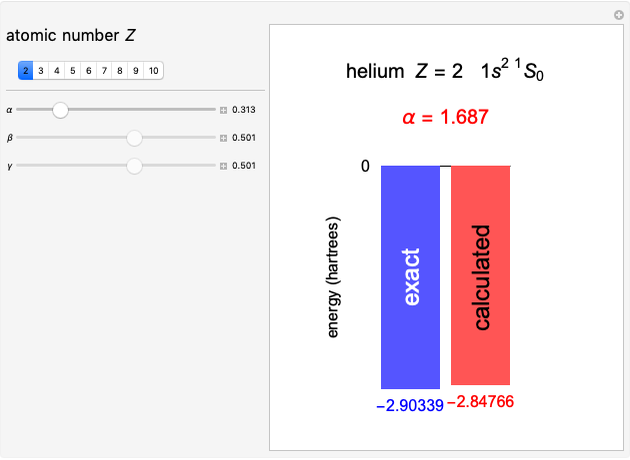
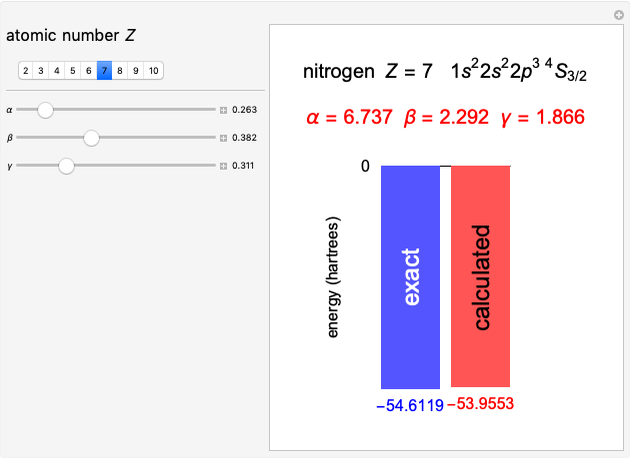
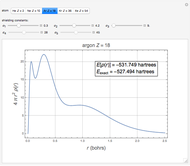
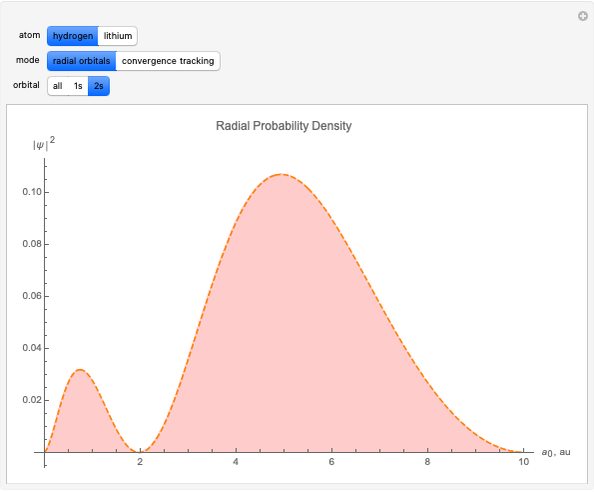
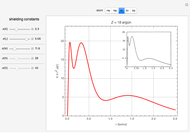
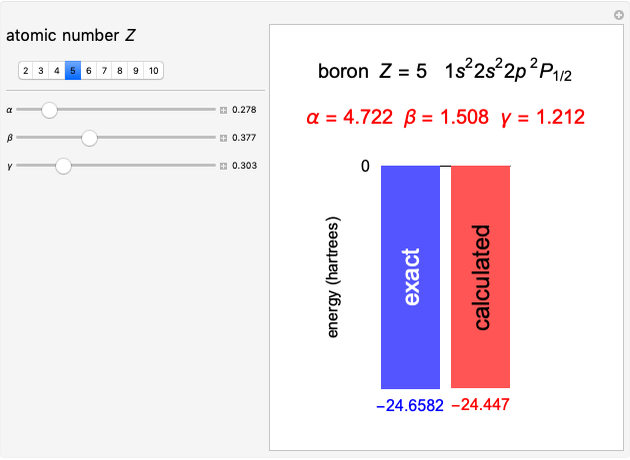
Following are results for optimized functions  ,
,  and
and  . For comparison we also include results from the best Hartree-Fock computations and the exact atomic ground-state energies.
. For comparison we also include results from the best Hartree-Fock computations and the exact atomic ground-state energies.

References
[1] S. M. Blinder, "Simplified Hartree-Fock Computations on Second-Row Atoms," https://arxiv.org/abs/2105.07018
[2] A. Szabo and N. S. Ostlund, Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory, Mineola, NY: Dover, 1996.
[3] S. M. Blinder, "Introduction to the Hartree–Fock Method," in Mathematical Physics in Theoretical Chemistry (S. M. Blinder and J. E. House, eds.), Elsevier, 2018.
Permanent Citation