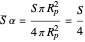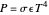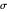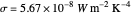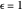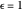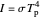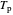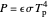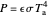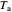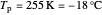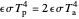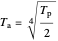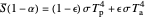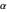Single-Layer Model for Planetary Atmospheres

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
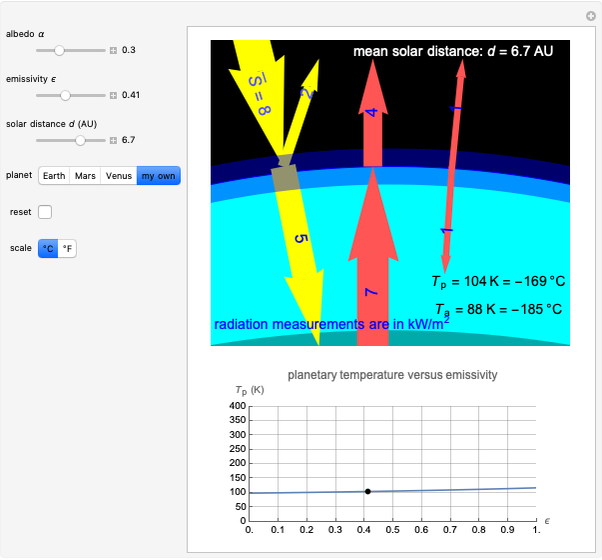
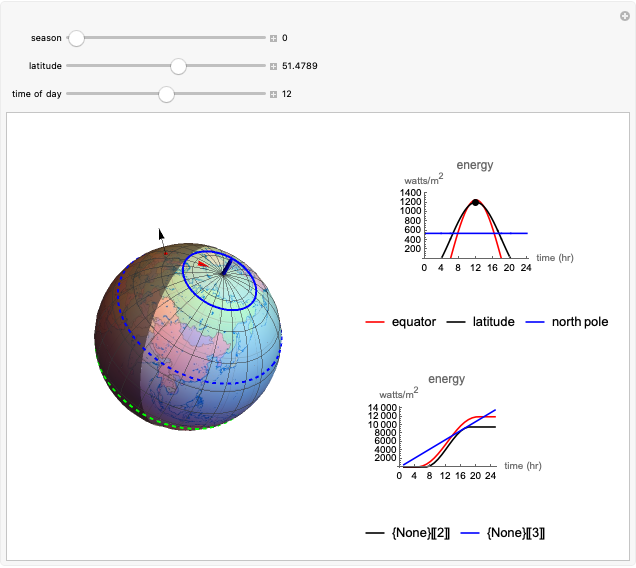
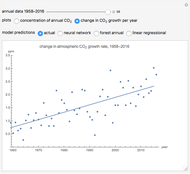
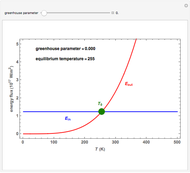
This Demonstration shows a simple single-layer model of the atmosphere of a planet. This layer diffusely reflects some fraction of incoming radiation and transmits the rest to the surface of the planet. The albedo  is the measure of this reflection. It can be varied by moving the slider: 0 corresponds to a blackbody that absorbs all radiation, 1 to a body that reflects all incident radiation. Thus if the incoming radiation is the average solar radiation per unit area
is the measure of this reflection. It can be varied by moving the slider: 0 corresponds to a blackbody that absorbs all radiation, 1 to a body that reflects all incident radiation. Thus if the incoming radiation is the average solar radiation per unit area 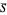 with a value of
with a value of 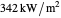 for Earth,
for Earth, 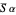 will be reflected and
will be reflected and 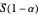 will reach the surface. It is assumed that all radiation that reaches the surface is absorbed by the planet. The average intensity can be calculated using
will reach the surface. It is assumed that all radiation that reaches the surface is absorbed by the planet. The average intensity can be calculated using
Contributed by: Sergio Hannibal Mejíaand Simon Lorimer (August 2022)
(Yokohama International School)
Open content licensed under CC BY-NC-SA
Snapshots
Details
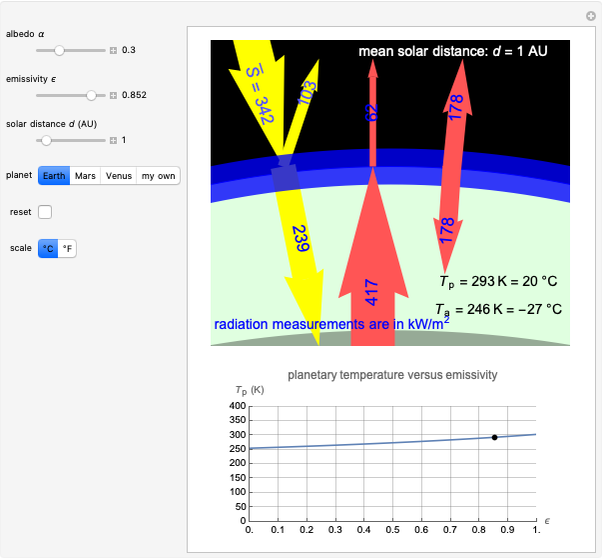
Snapshot 1: note the sensitivity of the temperature of the planet to small changes in emissivity; the mean temperature on Earth is now 15 °C (59 °F) [2]
Snapshot 2: select Mars and then reset for a good model for the Martian atmosphere; mean temperature on Mars is around -65 °C (85 °F) (Future Martian explorers, please remember to bring a good jacket!)
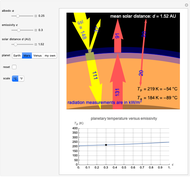
Snapshot 3: selecting Venus and then reset gives a rather poor model for the thick Venusian atmosphere; the measured temperature on Venus is 464 °C (-867 °F)
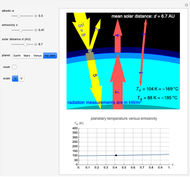
Snapshot 4: Europa, the smallest of the four Galilean moons orbiting Jupiter, has an emissivity of 0.94, and its mean distance from the Sun is 5 AU. The icy crust gives it an albedo of 0.64, the highest for all the moons in the solar system. Surface temperature reaches around 110 K. So our model seems quite accurate [3].
References
[1] ACS Chemistry for Life. "A Single-Layer Atmosphere Model." (May 20, 2022) www.acs.org/content/acs/en/climatescience/atmosphericwarming/singlelayermodel.html.
[2] NASA Planetary Fact Sheet. "Solar System Temperatures." (May 20, 2022) solarsystem.nasa.gov/resources/681/solar-system-temperatures.
[3] Y. Ashkenazy, "The Surface Temperature of Europa," Heliyon, 5(6), 2019 e01908. doi:10.1016/j.heliyon.2019.e01908.
Permanent Citation