Single-Slit Diffraction Pattern

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
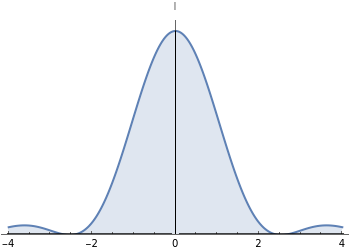
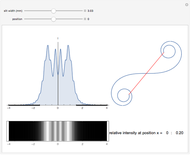
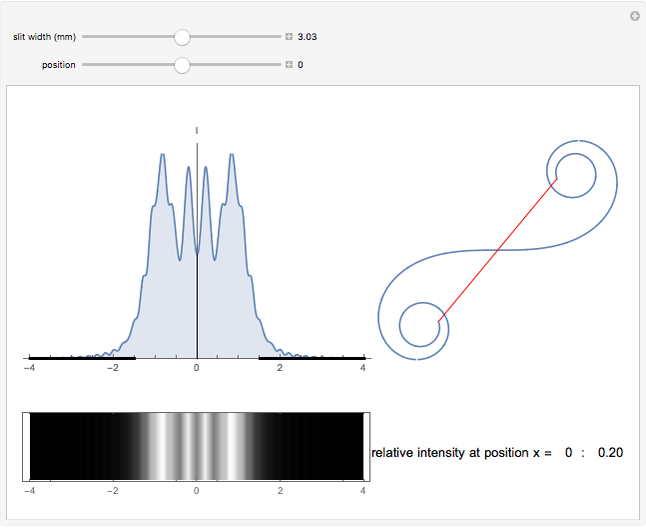
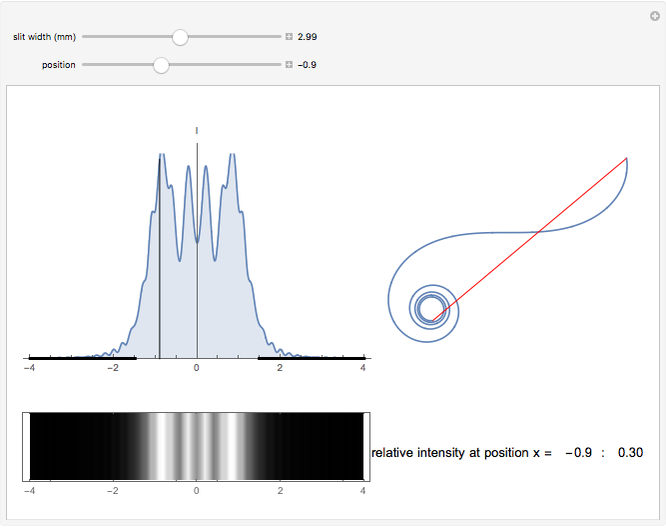
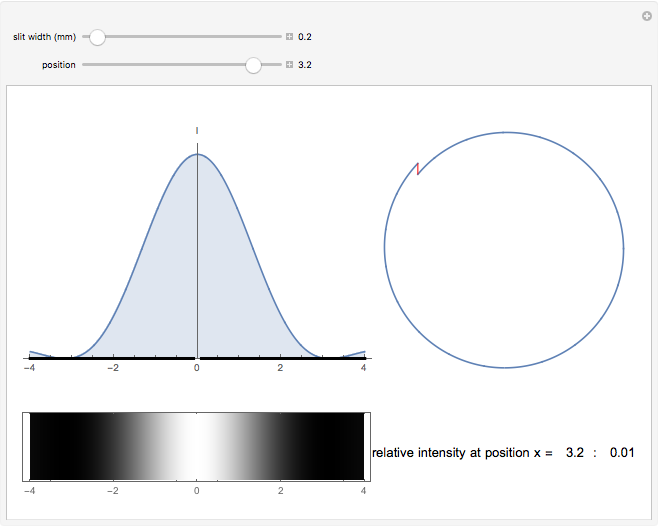
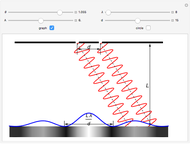
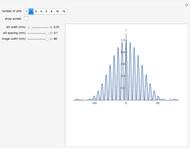
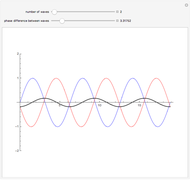
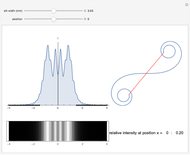
This Demonstration shows the intensity distribution of one-slit diffraction over a wide range of slit widths so that both Fraunhofer and Fresnel diffraction are covered. You can produce an interference pattern as it would be seen on a screen and the vector sum for any position on the screen. The results are derived from Feynman's method of "integrating over paths" and can be proven experimentally if the light source is a He-Ne laser and the screen is 1 m distance from the slit.
Contributed by: Hans-Joachim Domke and Martin Domke (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
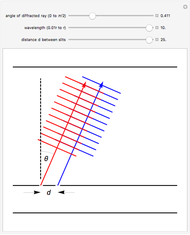
The aperture of the slit is divided into  points, each of which can be considered the origin of a wave. The wave vectors are summed up at a point on the screen. At a given point each wave has a different distance to travel, which results in a different phase angle
points, each of which can be considered the origin of a wave. The wave vectors are summed up at a point on the screen. At a given point each wave has a different distance to travel, which results in a different phase angle  . Let
. Let  be the distance between the slit and the screen,
be the distance between the slit and the screen,  the distance of the point on the screen relative to the optic axis and
the distance of the point on the screen relative to the optic axis and  the space between one of the points in the slit to the optic axis. The length of a path is then
the space between one of the points in the slit to the optic axis. The length of a path is then  . Because
. Because  it is approximately
it is approximately  . In the case of Fraunhofer diffraction where the slit width
. In the case of Fraunhofer diffraction where the slit width  it can be further approximated to
it can be further approximated to  , which means that
, which means that  and hence
and hence  depend linearly on
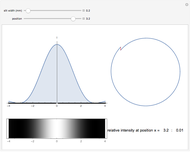
depend linearly on  . The sum of the wave vectors gives a line of constant curvature, a circle. It is completed for the first time in the first minima. When
. The sum of the wave vectors gives a line of constant curvature, a circle. It is completed for the first time in the first minima. When  becomes greater,
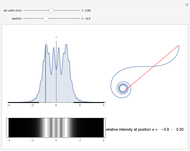
becomes greater,  cannot be neglected and the phase angle between two neighboring wave vectors is no longer constant. The result of the vector sum is now the so-called
cannot be neglected and the phase angle between two neighboring wave vectors is no longer constant. The result of the vector sum is now the so-called  spiral, which is an important tool for investigating Fresnel diffraction.
spiral, which is an important tool for investigating Fresnel diffraction.
 After the French physicist Alfred Cornu (1841-1902).
After the French physicist Alfred Cornu (1841-1902).
R. P. Feynman, QED: The Strange Theory of Light and Matter, Princeton: Princeton University Press, 1985.
Permanent Citation