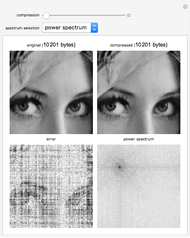
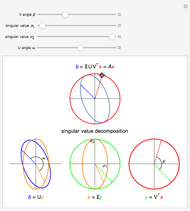
Singular Value Decomposition
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
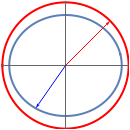
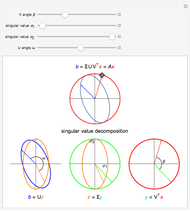
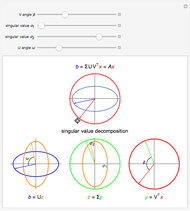
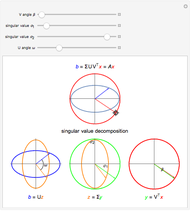
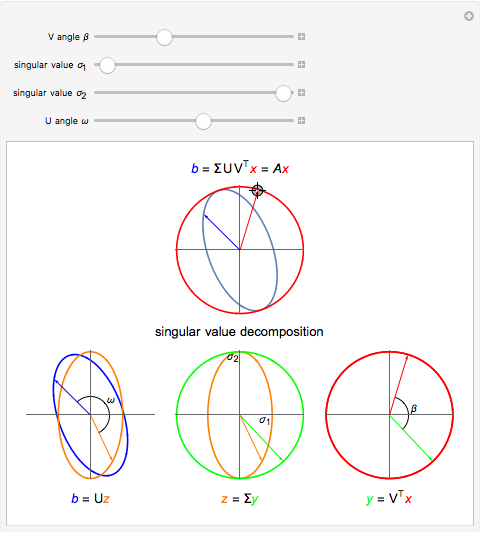
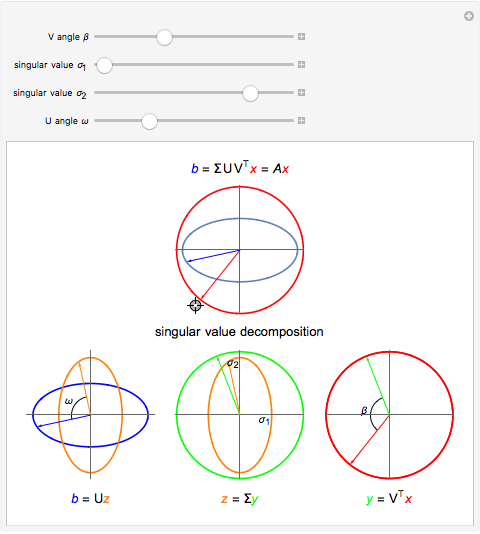
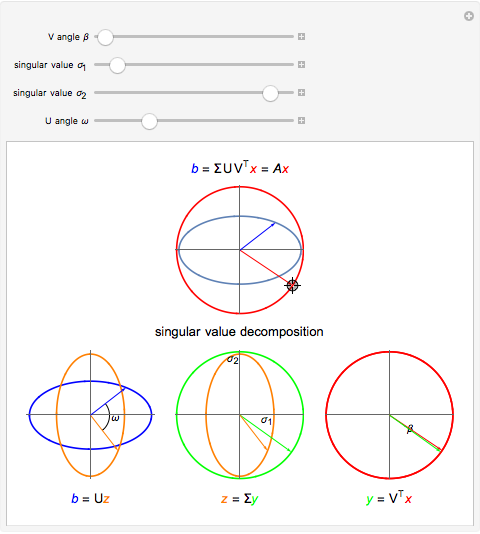
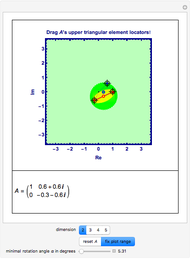
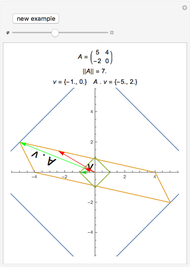
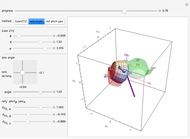
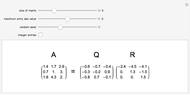
The singular value decomposition is a factorization of a matrix 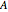 into
into 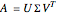 . A vector
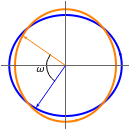
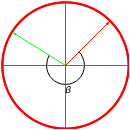
. A vector  is first rotated by an angle β via
is first rotated by an angle β via 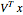 , then
, then 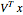 is scaled by a diagonal matrix
is scaled by a diagonal matrix  to form
to form 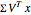 . Finally the vector
. Finally the vector 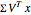 is rotated by an angle ω to form
is rotated by an angle ω to form 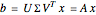 .
.
Contributed by: Chris Maes (March 2011)
Open content licensed under CC BY-NC-SA
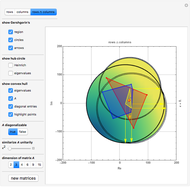
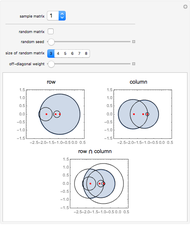
Snapshots
Details
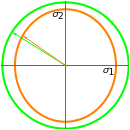
Note that U and V are orthogonal matrices and thus do not alter the length of the vectors. In 2D the diagonal matrix Σ has the form
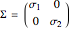
here 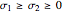 are the singular values of the matrix.
are the singular values of the matrix.
Permanent Citation