Skin Effects in Straight Wires

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
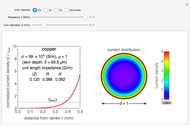
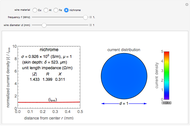
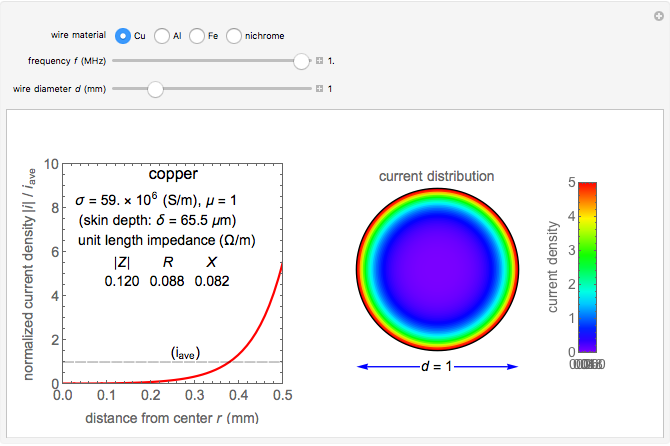
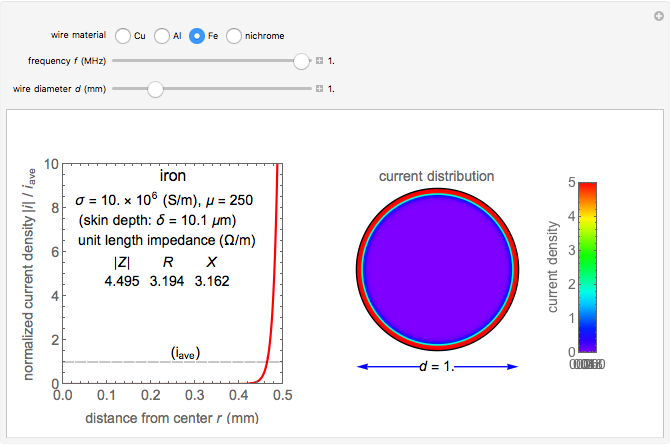
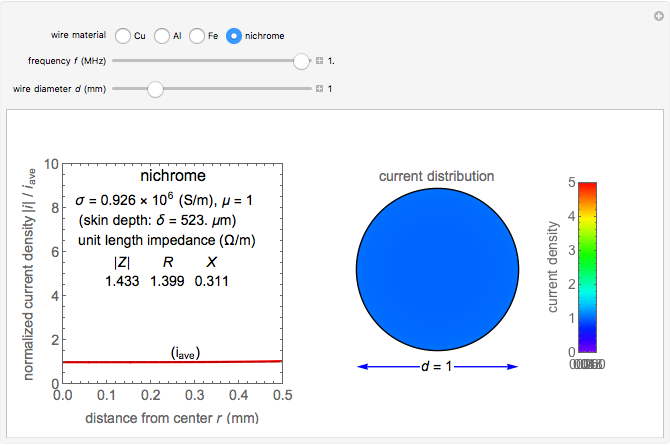
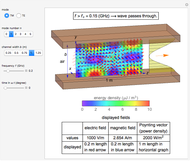
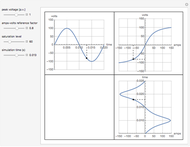
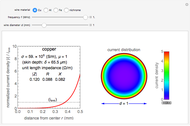
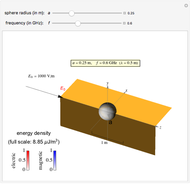
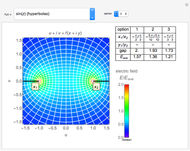
A wire carrying high-frequency currents is subject to the skin effect: most of the current flows near the outside of the wire. Assuming a sinusoidal current in a cylindrical straight wire of infinite length, the sectional current distribution is formulated using Bessel functions, which is determined by the wire's material properties, frequency, and diameter. The conductivity and permeability of the wire's material are relevant to the skin effect.
[more]
Contributed by: Y. Shibuya (November 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: nonuniform current distribution for 1 mm copper wire at 1 MHz
Snapshot 2: more nonuniform current distribution for iron wire
Snapshot 3: uniform current distribution for nichrome wire
The conductivities for the four materials are typical values at room temperature. The specific permeability  is the typical initial permeability of pure iron.
is the typical initial permeability of pure iron.
For the sinusoidal current  of angular velocity
of angular velocity  flowing in the wire of radius
flowing in the wire of radius  , the current density at radius
, the current density at radius  is given by
is given by  , where
, where  . The output in the graphics is normalized to an average current density
. The output in the graphics is normalized to an average current density  . The impedance per unit length
. The impedance per unit length  is derived by dividing the outermost electric field
is derived by dividing the outermost electric field  by the current
by the current  .
.
The analysis associated with skin effect is a quasistatic field problem in which fields are governed by the diffusion equation  (or in terms of current density,
(or in terms of current density,  ). The above harmonic solution is obtained considering the cylindrically symmetric solution of this diffusion equation. The diffusion equation corresponds to the Maxwell equation neglecting the displacement current.
). The above harmonic solution is obtained considering the cylindrically symmetric solution of this diffusion equation. The diffusion equation corresponds to the Maxwell equation neglecting the displacement current.
Permanent Citation