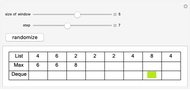
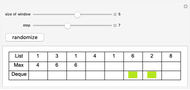
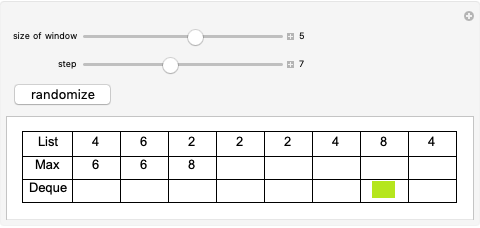
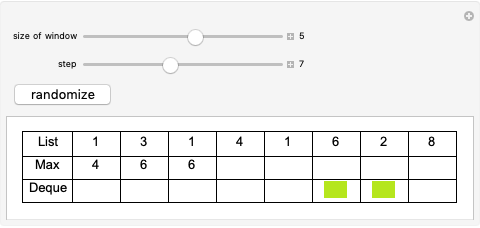
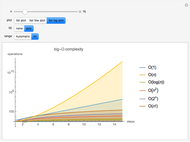
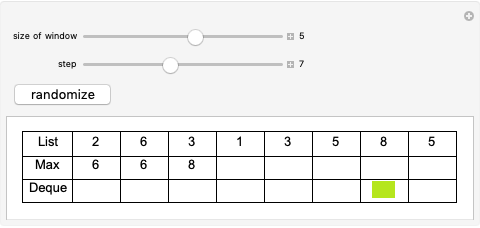
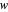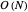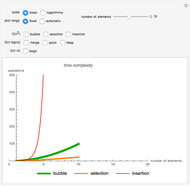
The displayed algorithm calculates the sliding window maximums, the maximum on any given contiguous subset of window size in the array, of the given array of integers in . While this problem seems fairly trivial at first, the naive solution to the problem results in a 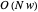solution. As such, using this algorithm results in a speed up by a factor of 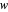. The first row represents the array while the second row represents the array of currently calculated maximums as the program steps through the algorithm. The final row is an indication as to whether the elements are in the deque (double-ended queue) or not. The actual algorithm achieves 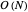time by using a deque and putting and popping each element off exactly once, resulting in an amortized 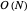. At each step in the algorithm, the front of the deque is checked for being larger than the current element. If not, it is popped off, and the back of the deque is also popped off if it is outside the window.