Solving a Cubic via the Trisection of an Angle
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
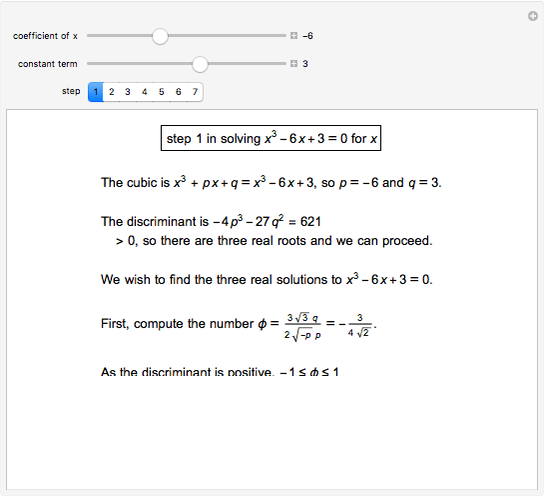
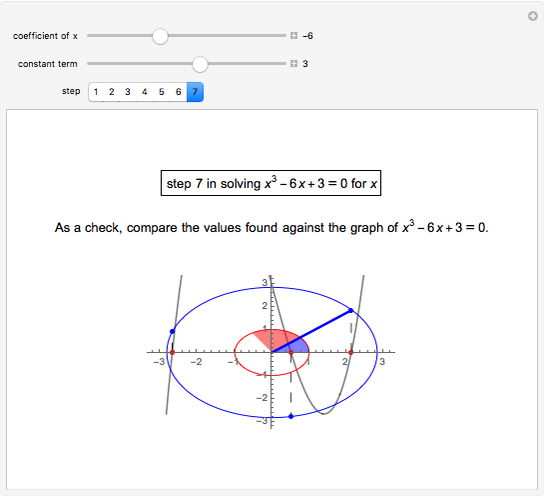
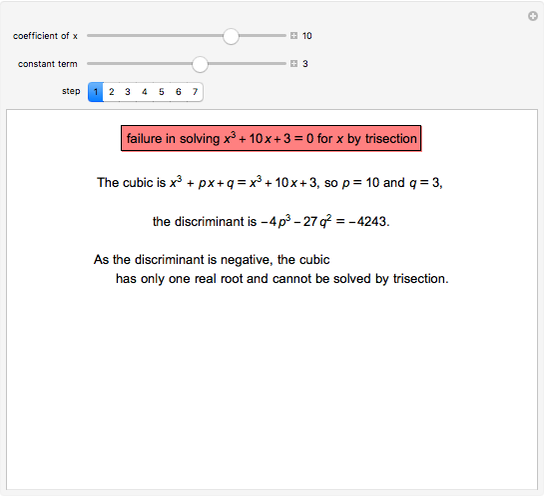
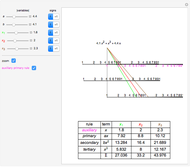
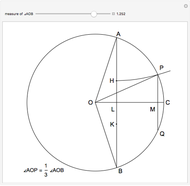
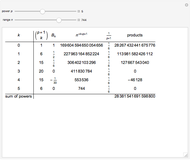
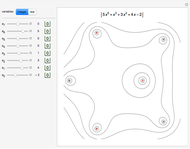
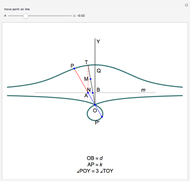
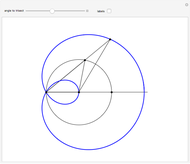
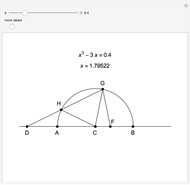
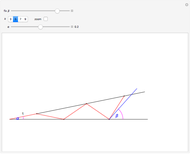
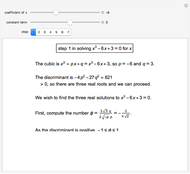
This Demonstration shows a geometric solution to the equation 
, where 
and 
are real in the case where the equation has three distinct real roots (i.e. has a positive discriminant). It is based on Viète's trigonometric solution of the cubic that constructs and trisects a particular angle associated with the given cubic equation.
Contributed by: Christopher Moretti (October 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For a detailed discussion of the trigonometric solution to the cubic, see [1] or [2].
References
[1] G. E. Martin, Geometric Constructions, New York: Springer–Verlag, 1998 p. 132–133.
[2] D. A. Cox, Galois Theory, New York: John Wiley & Sons, 2004 p. 18–19.
Permanent Citation
Newton's Polynomial Solver
Izidor Hafner
Descartes's Angle Trisection
Izidor Hafner
Pascal's Angle Trisection
Izidor Hafner
Clairaut's Angle Trisection
Izidor Hafner
Using Bernoulli's Formula to Sum Powers of the Integers from 1 to n
Ed Pegg Jr
The Fundamental Theorem of Algebra
Ed Pegg Jr
Trisecting an Angle Using a Conchoid
Izidor Hafner
Trisecting an Angle with a Limaçon
Izidor Hafner
Vieta's Solution of a Cubic Equation
Izidor Hafner
Generalized Trisection Construction
Izidor Hafner
