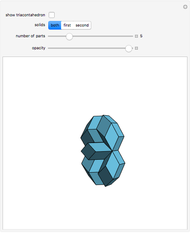
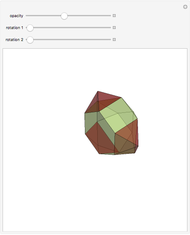
Some Archimedean Solids in the Icosahedral Lattice

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
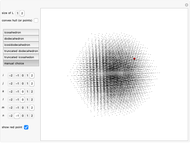
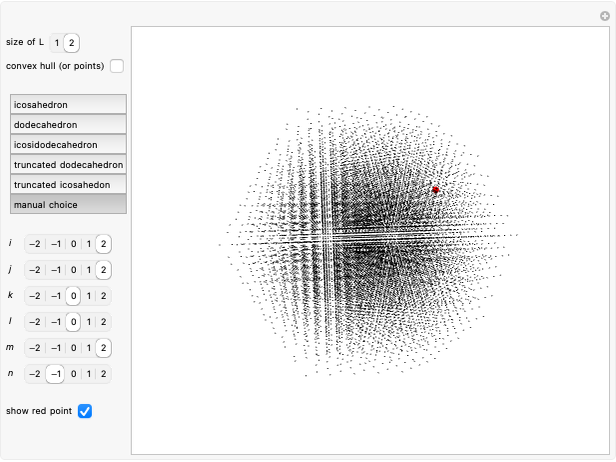
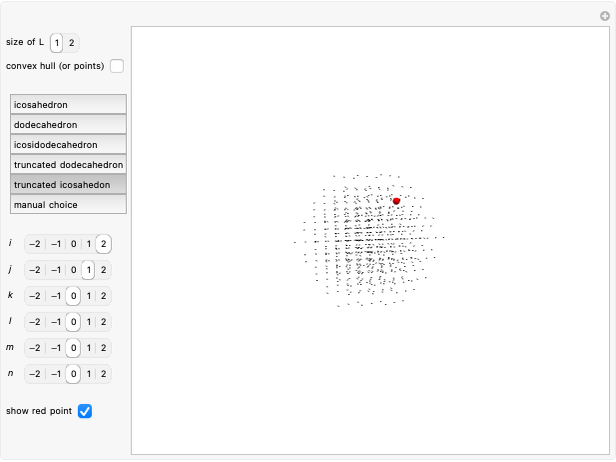
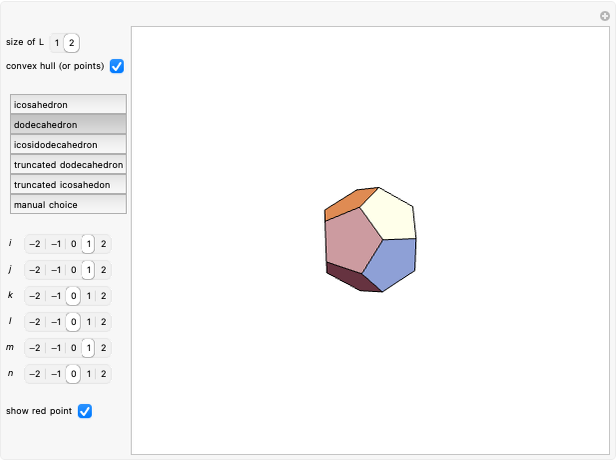
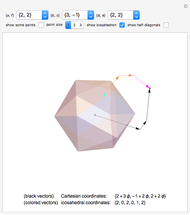
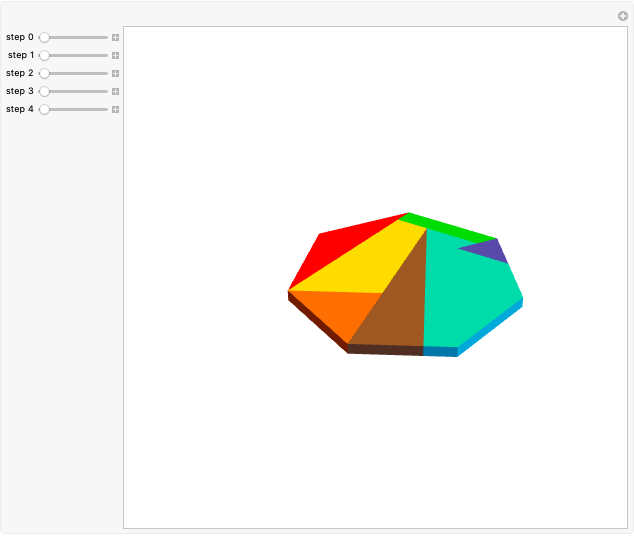
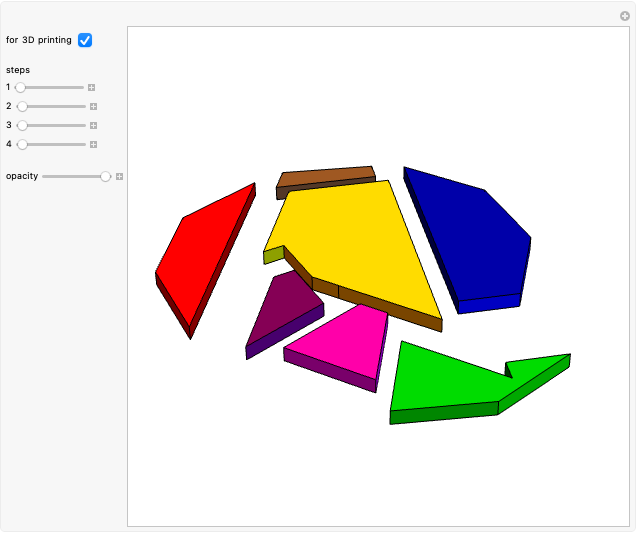
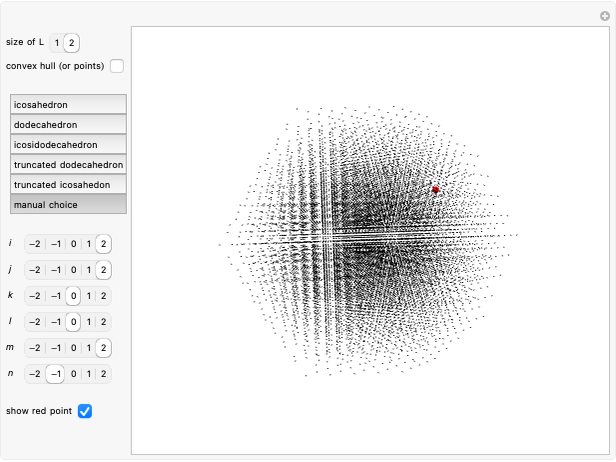
This Demonstration considers a set of points 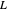 of integral linear combinations
of integral linear combinations 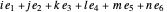 , where the
, where the 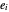 are six vertices of a regular icosahedron and the coefficients
are six vertices of a regular icosahedron and the coefficients  to
to 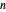 are integers between
are integers between 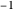 and
and  or
or 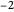 and
and 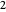 , for a total of
, for a total of 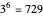 or
or 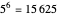 points. The coordinates of the
points. The coordinates of the 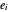 are the six permutations of
are the six permutations of  ,
,  , and
, and 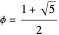 (the golden ratio). The convex hull of
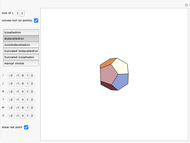
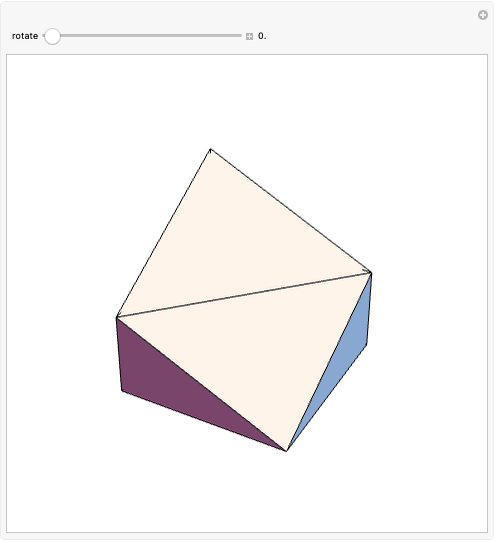
(the golden ratio). The convex hull of  is a triacontahedron. Certain choices of linear combinations give the vertices of a dodecahedron, an icosidodecahedron, a truncated dodecahedron, and a truncated icosahedron. Given one vertex on a solid, all the other vertices are points in
is a triacontahedron. Certain choices of linear combinations give the vertices of a dodecahedron, an icosidodecahedron, a truncated dodecahedron, and a truncated icosahedron. Given one vertex on a solid, all the other vertices are points in  that are at the same distance as the given one.
that are at the same distance as the given one.
Contributed by: Izidor Hafner (April 2013)
Open content licensed under CC BY-NC-SA
Details
The set of all triplets 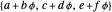 with integer coefficients is called phi space.
with integer coefficients is called phi space.
Snapshots
Permanent Citation