Sounds of Waveforms

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
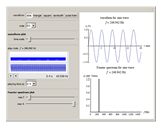
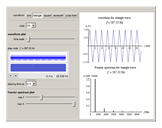
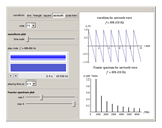
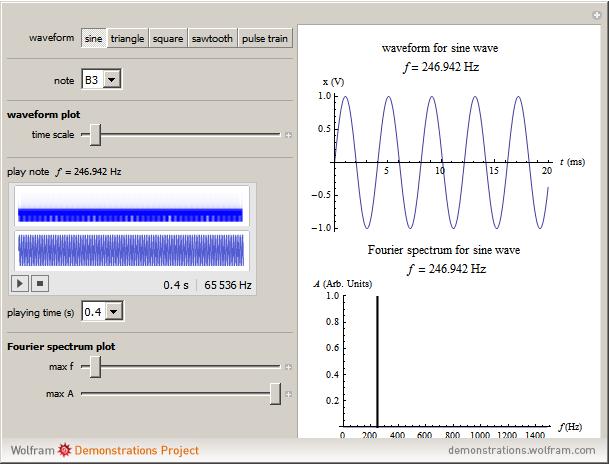
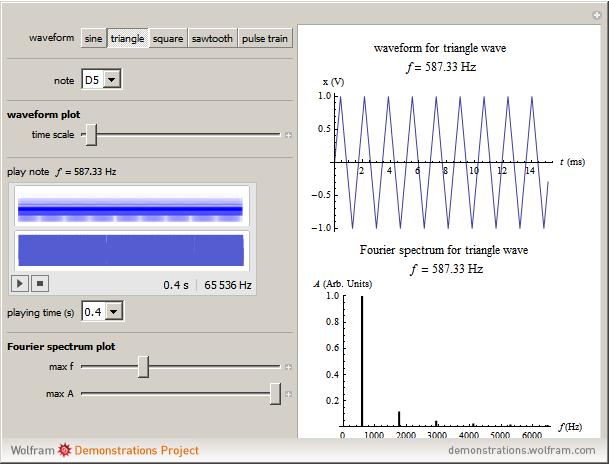
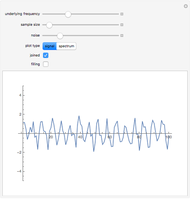
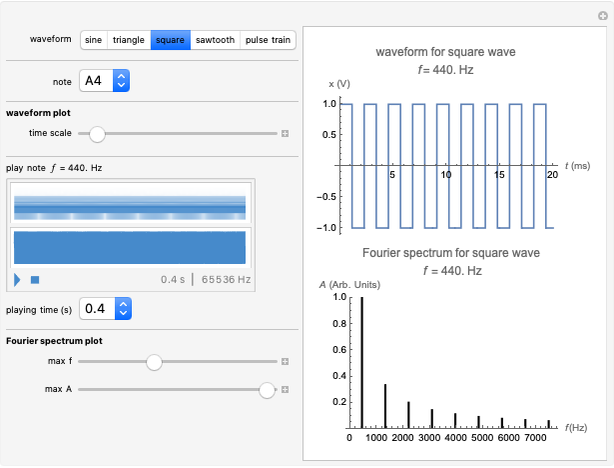
Choose a waveform and note, listen to its sound, and look at the plots of the waveform and the Fourier spectrum. Notice that the tone quality of the sound changes with the changing waveform. Try this for various notes. As you change the selected note, you can use the sliders to change the time scale on the waveform plot and the maximum frequency and maximum amplitude on the Fourier spectrum plot to get a better view.
Contributed by: Marilyn F. Bishop (Virginia Commonwealth University, Department of Physics and Center for the Study of Biological Complexity, Richmond, Virginia) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration is useful for understanding how the addition of harmonics of a fundamental note can change the tone quality of a note. According to Ohm's law of hearing, the amplitudes of the harmonics, as seen in the Fourier spectrum plot, have the most influence in determining the tone quality of a sustained note. The harmonics are integer multiples of the fundamental:  ,
,  ,
,  ,
,  , etc. The sine wave contains only the single fundamental frequency
, etc. The sine wave contains only the single fundamental frequency  , as seen by the single spike in the Fourier spectrum, which occurs at the position of the fundamental frequency (considered to be the pitch of the note). The lack of complexity of its sound makes it seem electronic. The triangle wave and square wave have only odd harmonics:
, as seen by the single spike in the Fourier spectrum, which occurs at the position of the fundamental frequency (considered to be the pitch of the note). The lack of complexity of its sound makes it seem electronic. The triangle wave and square wave have only odd harmonics:  ,
,  ,
,  ,
,  , etc., while the sawtooth and pulse train have all harmonics:
, etc., while the sawtooth and pulse train have all harmonics:  ,
,  ,
,  ,
,  , etc. These waveforms also differ from each other by the relative amplitudes of their harmonics or the relative heights of the spikes in their Fourier spectra. The triangle wave Fourier amplitudes are
, etc. These waveforms also differ from each other by the relative amplitudes of their harmonics or the relative heights of the spikes in their Fourier spectra. The triangle wave Fourier amplitudes are  for
for  ,
,  for
for  ,
,  for
for  ,
,  for
for  ,
,  for
for  , etc. For the square wave, the Fourier amplitudes are
, etc. For the square wave, the Fourier amplitudes are  for
for  ,
,  for
for  ,
,  for
for  ,
,  for
for  ,
,  for
for  , etc. The sawtooth, with all harmonics, has Fourier amplitudes
, etc. The sawtooth, with all harmonics, has Fourier amplitudes  for
for  ,
,  for
for  ,
,  for
for  ,
,  for
for  ,
,  for
for  , etc. The pulse train has the same amplitude for all harmonics.
, etc. The pulse train has the same amplitude for all harmonics.
Understanding the waveforms, Fourier spectra, and corresponding sounds of these simple waveforms gives insight into the difference in tone quality and design of musical instruments. For instance, the sound of the clarinet, which is roughly a cylindrical tube with one end closed (the reed end) and the other end open (the bell), is dominated by the odd harmonics, which gives it a characteristic sound somewhat like that of a square wave. On the other hand, the sound of the flute, which is roughly a cylindrical tube open at both ends, is completely different because all harmonics are present.
R. E. Berg and D. G. Stork, The Physics of Sound, 3rd ed., Upper Saddle River, NJ: Prentice Hall, 2005.
D. E. Hall, Musical Acoustics, 3rd ed., Pacific Grove, CA: Thompson Learning Brooks/Cole, 2002.
T. D. Rossing, F. R. Moore, and P. A. Wheeler, The Science of Sound, 3rd ed., San Francisco: Addison Wesley, 2002.
Permanent Citation
"Sounds of Waveforms"
http://demonstrations.wolfram.com/SoundsOfWaveforms/
Wolfram Demonstrations Project
Published: March 7 2011