Spectra of the D-Lines of Alkali Vapors

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
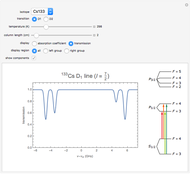
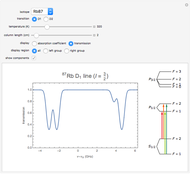
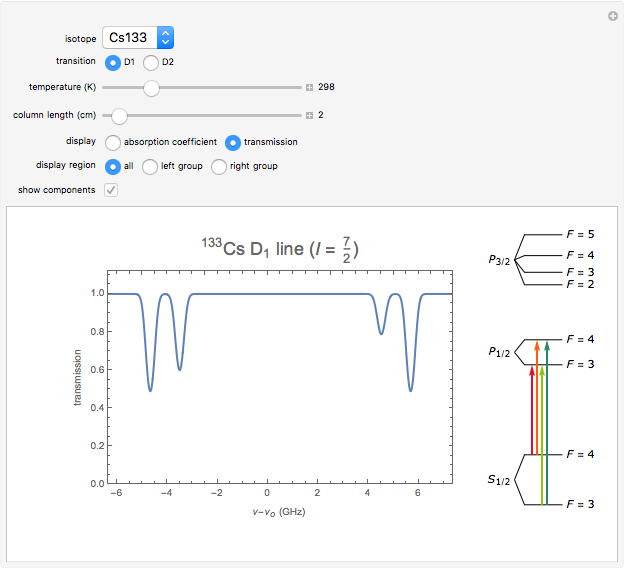
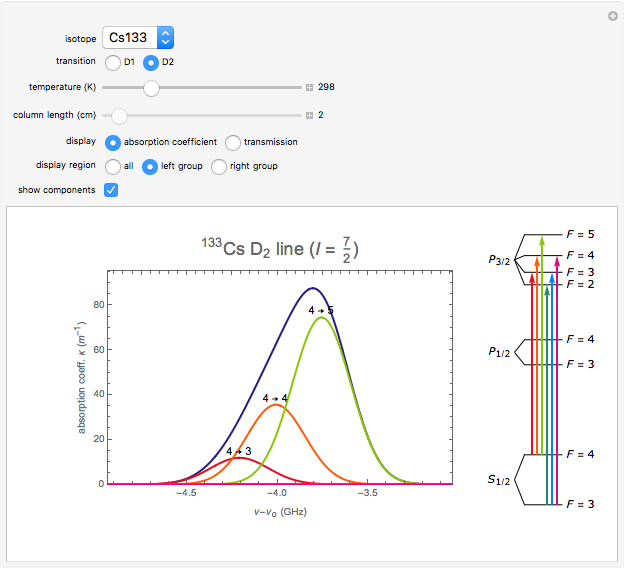
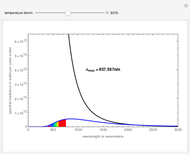
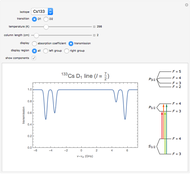
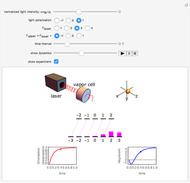
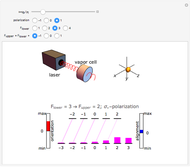
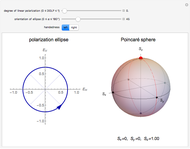
This Demonstration represents the spectra of alkali atoms, that is, the frequency dependence of the optical absorption coefficient  and the transmission
and the transmission  of a vapor column (length
of a vapor column (length  ). Spectra are shown for light tuned near the
). Spectra are shown for light tuned near the  (
( ) and
) and  (
( ) transitions for the most abundant alkali isotopes. The calculation takes the hyperfine structure into account and assumes a pure Doppler broadening of the lines. You can vary the column length
) transitions for the most abundant alkali isotopes. The calculation takes the hyperfine structure into account and assumes a pure Doppler broadening of the lines. You can vary the column length  as well as the atomic density, which is controlled via the temperature‐dependent saturated vapor pressure. The level scheme on the right shows the involved (allowed) individual hyperfine transitions that contribute to the spectrum.
as well as the atomic density, which is controlled via the temperature‐dependent saturated vapor pressure. The level scheme on the right shows the involved (allowed) individual hyperfine transitions that contribute to the spectrum.
Contributed by: Gianni Di Domenico (Université de Neuchâtel) and Antoine Weis (Université de Fribourg) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The power  of a light beam traversing an atomic vapor is attenuated to a value
of a light beam traversing an atomic vapor is attenuated to a value  . The transmission
. The transmission  can be parametrized in terms of the absorption coefficient
can be parametrized in terms of the absorption coefficient  and the vapor column length
and the vapor column length  according to the Lambert-Beer law as
according to the Lambert-Beer law as  .
.
The absorption coefficient  depends on the detuning of the light frequency
depends on the detuning of the light frequency  from the atomic resonance frequency
from the atomic resonance frequency  . Under the assumption of pure Doppler broadening, the absorption coefficient near the resonance frequency of a transition from a ground state
. Under the assumption of pure Doppler broadening, the absorption coefficient near the resonance frequency of a transition from a ground state  to an excited state
to an excited state  is given by
is given by

where  is the atomic density,
is the atomic density,  the wavelength of the transition,
the wavelength of the transition,  the lifetime of the excited state, and the Doppler width is
the lifetime of the excited state, and the Doppler width is
 ,
,
with the vapor temperature T and the atomic mass  , and where
, and where

are the relative intensities of the hyperfine components with  being the nuclear spin. The symbols on the right of the last equation represent Racah 6-
being the nuclear spin. The symbols on the right of the last equation represent Racah 6- symbols.
symbols.
The atomic density is inferred from the vapor pressure  by assuming the ideal gas relations. The vapor pressure is parametrized in the Clausius-Clapeyron form
by assuming the ideal gas relations. The vapor pressure is parametrized in the Clausius-Clapeyron form  , which assumes a thermodynamic equilibrium between the bulk metal and its vapor, and where the constants
, which assumes a thermodynamic equilibrium between the bulk metal and its vapor, and where the constants  and
and  depend on the isotope and on the state of aggregation (solid or liquid) of the bulk (see Vapor Pressure and Density of Alkali Metals for details).
depend on the isotope and on the state of aggregation (solid or liquid) of the bulk (see Vapor Pressure and Density of Alkali Metals for details).
Spectra are then obtained by summing the contributions (1) of all allowed hyperfine components  of the transition with resonance frequencies given by the hyperfine structure of the coupled states.
of the transition with resonance frequencies given by the hyperfine structure of the coupled states.
Permanent Citation