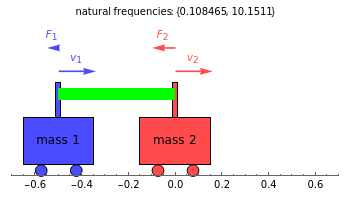
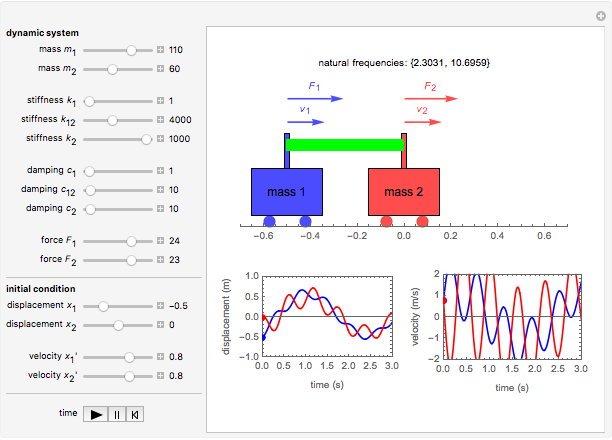
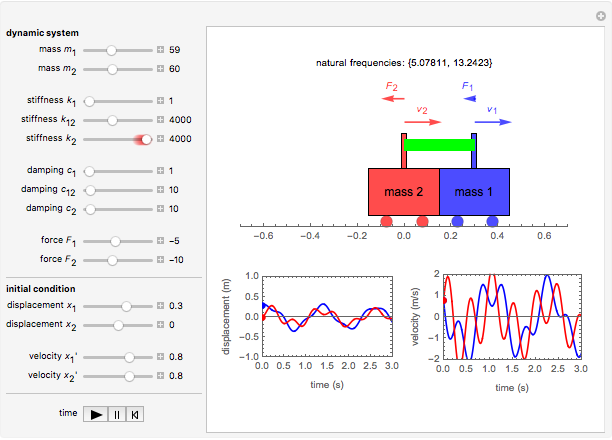
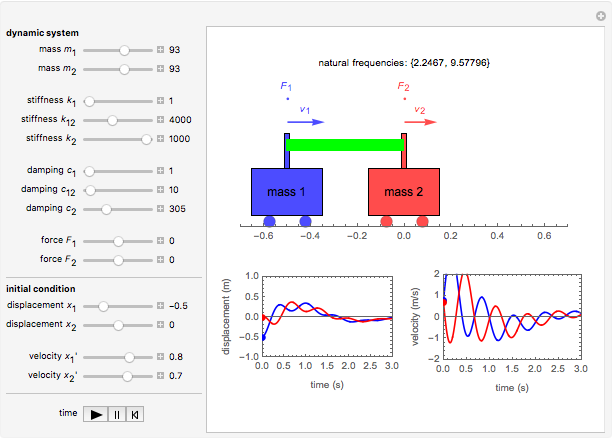
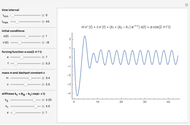
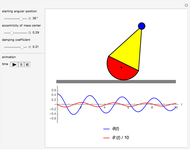
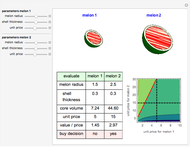
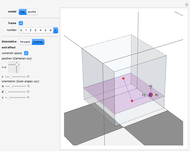
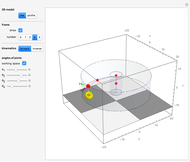
This Demonstration shows the dynamics of a spring-mass-damping system with two degrees of freedom under external forces. The motion of the system is represented by the positions and of the masses and at time . Both masses have a spring connected to a stationary base, with spring constants and ; also for the spring connecting the two masses. The motion of the masses is damped, with damping factors and ; also for damping between the two masses. The masses are acted upon by external forces and .