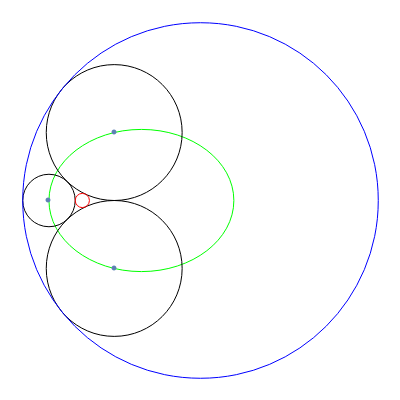
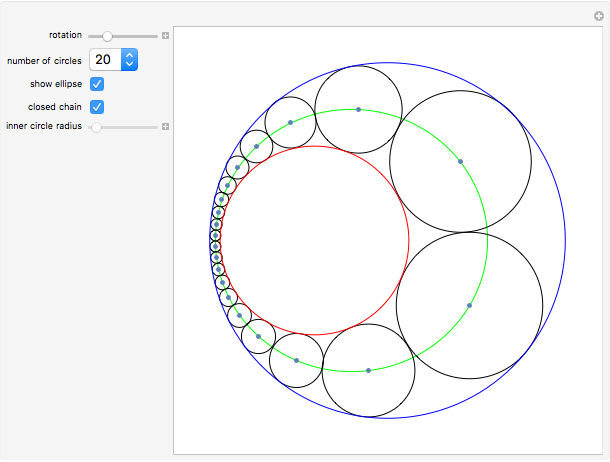
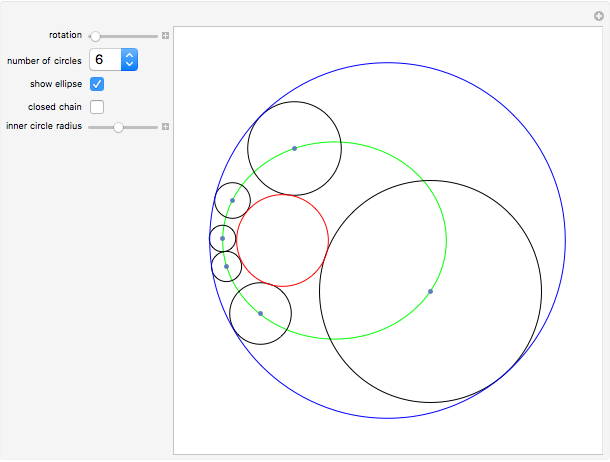
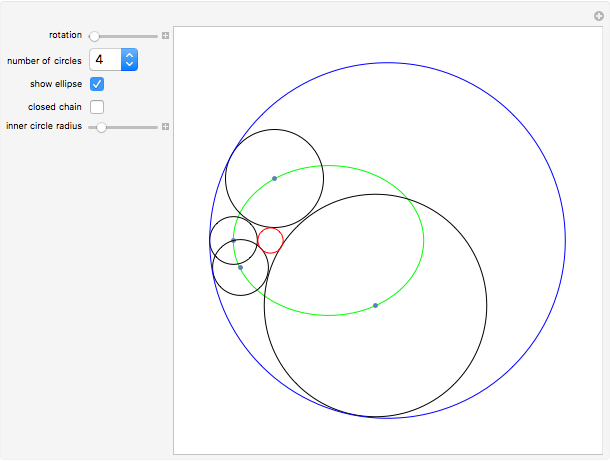
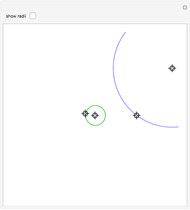
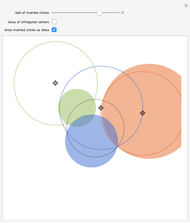
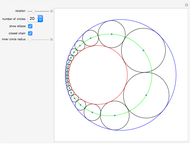
Given two fixed nonintersecting circles (shown here in red and blue), a Steiner chain is a sequence of circles, each tangent to the two given circles and each tangent to their neighboring circles in the sequence. When the chain is closed, the first and last circles in the chain are also tangent to each other. If a closed chain can be found for a given pair of circles, then infinitely many such chains can be found—use the rotation slider. Also, regardless of whether the chain is open or closed, the centers of circles of the chain lie on an ellipse, shown in green.