Steinhaus' Billiard Ball Loop

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
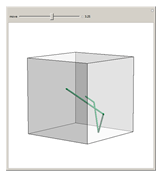
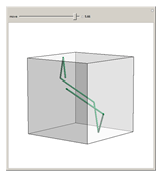
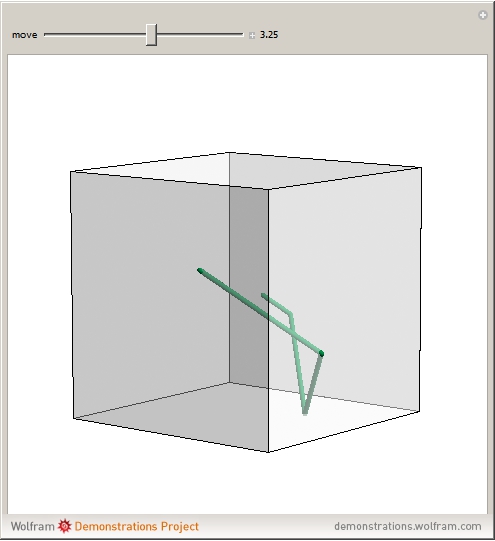
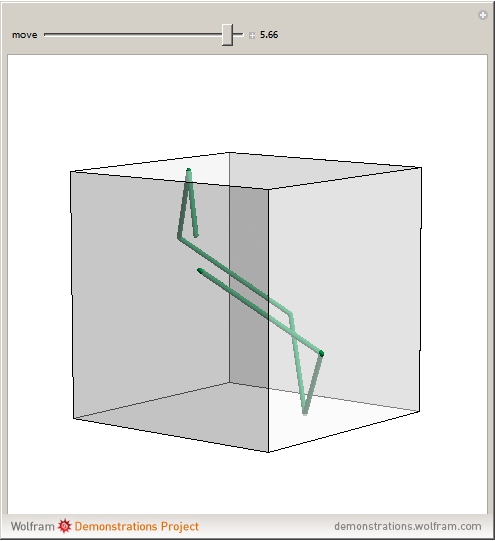
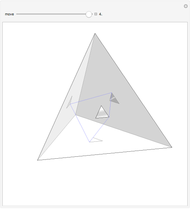
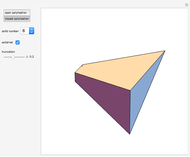
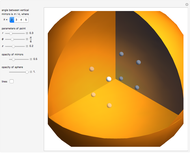
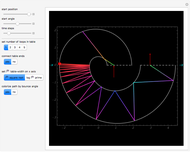
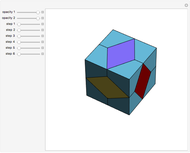
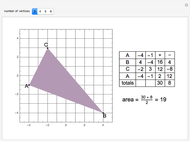
A billiard path is a polygon with vertices on the faces of a polyhedron such that if two segments meet at a vertex  on a face
on a face  , the plane through them is perpendicular to
, the plane through them is perpendicular to  and the angle they form is bisected by the normal to
and the angle they form is bisected by the normal to  at
at  . A billiard ball loop is a closed billiard path.
. A billiard ball loop is a closed billiard path.
Contributed by: Izidor Hafner (October 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] D. Wells, The Penguin Dictionary of Curious and Interesting Geometry, London: Penguin Books, 1991, pp. 13–14.
Permanent Citation
"Steinhaus' Billiard Ball Loop"
http://demonstrations.wolfram.com/SteinhausBilliardBallLoop/
Wolfram Demonstrations Project
Published: October 15 2013