Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Stochastic Diploid Model for Gene Frequency in a Population

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

Imagine a single gene with two alleles 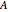and , where the frequency of the 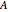allele in the gene pool of an entire population is 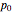. Assume that this is a large and isolated population, that there is random mating, and that the fitness parameter varies stochastically through the generations. One can then predict the frequency of the 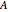allele in the population after generations.

[more]

This Demonstration gives the time series of and lets you vary the fitness parameter and the stochastic noise . By moving the sliders, you can see that for a fixed there is a critical value of beyond which polymorphism (the existence of two or more different phenotypes in the population) occurs as a result of stochastic resonance. The dynamics does not depend on the initial condition .

[less]

Contributed by: Sujatha Ramakrishnan (November 2015)
(IISERTVM)
Open content licensed under CC BY-NC-SA

Snapshots

Details

J. B. S. Haldane (1924) proposed a model for the gene frequency of two phenotypes in a population. Let a pair of alleles 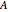and occur in the ratio .

Let be fully recessive as regards fitness and let the fitness of in the year relative to and be a stochastic parameter .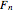

Then ,

or equivalently,

,

where is the fraction of dominant allele and .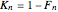

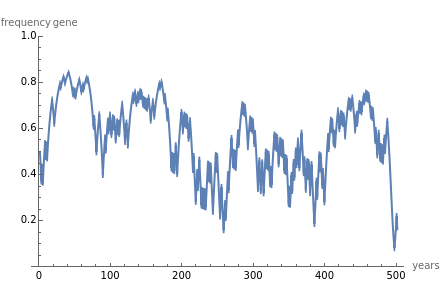
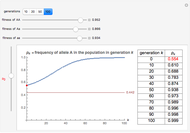
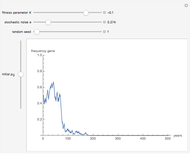
Haldane showed that polymorphism can be seen in the population as long as the geometric mean of 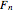is less than 1.

In this Demonstration, is eithe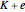r or each year with equal probability 1/2. So the condition for polymorphism is 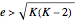. This Demonstration shows a time series for . By varying for a fixed fitness parameter , emergence of polymorphism can be seen at noise level .

Reference

[1] J. B. S. Haldane and S. D. Jayakar, "Polymorphism Due to Selection of Varying Direction," Journal of Genetics, 58(2), 1963 pp. 237–242. doi:10.1007/BF02986143.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send