Stochastic Rock-Paper-Scissors Population Dynamics

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
When three strategies (A, B, and C) compete for the same resources, a property called cyclic dominance can often be observed: the presence of As hinders the reproduction of Bs, Bs have an adverse effect on the reproduction of Cs, and Cs have a similar advantage over As. Real-life examples have been studied in colonies of bacteria (Kerr et al., 2002) and in lizard populations (Sinervo and Lively, 1996). You can examine the oscillating population structure that results from this rule and find out why random effects have a critical influence, as derived in (Reichenbach et al., 2006; 2008), by running this real-time simulation.
Contributed by: Martin Weidl (March 2011)
Suggested by: Erwin Frey and Jonas Cremer
After work by: Tobias Reichenbach, Mauro Mobilia, and Erwin Frey
Open content licensed under CC BY-NC-SA
Snapshots
Details
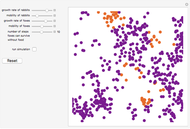
The core assumption of the rock-paper-scissors model is that members of the A species survive longer in populations with higher B counts ("A beats B") and lower C counts ("C beats A"), and that cyclic equivalents of this rule hold for the B and C survival rates.
In an ecosystem dominated by As, for example, the B population will dwindle. Since this makes it easier for Cs to multiply, however, the A count will suffer in the long term, helping the B species to recover, etc. These oscillations would continue ad infinitum in a simple deterministic model, although with ever-increasing amplitudes.
To mirror the random influences that always affect real ecosystems, evolutionary selection (death) and reproduction can both be modeled as separate "chemical reactions" that occur randomly in a four-type population (A, B, C, and "empty" for any unused resources in the ecosystem):
1. In a reproduction process, two random individuals are chosen. If either one is "empty", it is replaced with the species of the other individual.
2. A selection process only occurs if two randomly chosen individuals belong to different species. Then, the weaker one (in the sense of the rock-paper-scissors principle described above) is replaced with "empty".
The resulting deviations from the deterministic case described above may be small, especially for large populations, but eventually a species with low population count will become extinct. As one of the remaining species has a clear advantage over the other one due to the rock-paper-scissors rules, the game now has an obvious winner that will be able to take over all of the system.
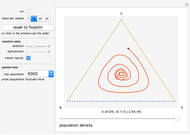
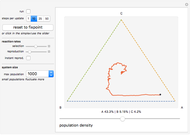
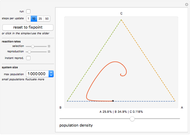
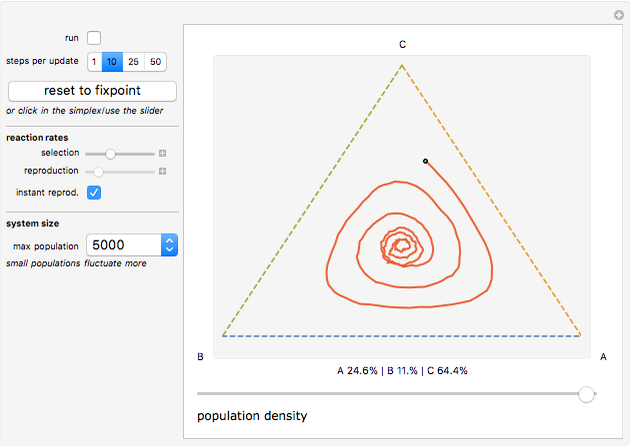
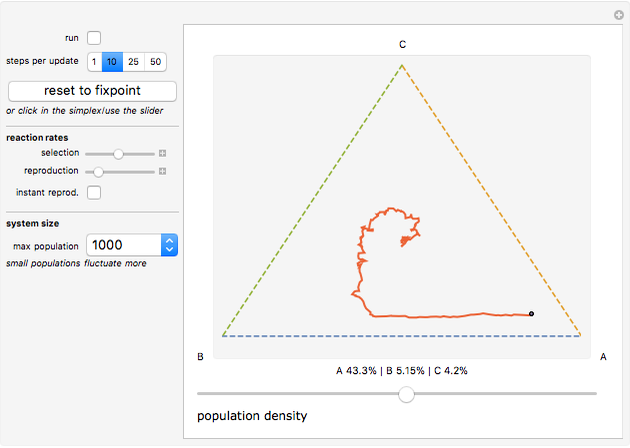
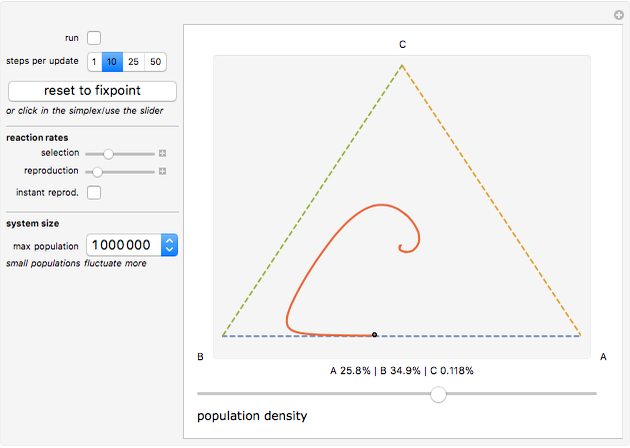
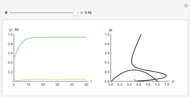
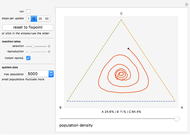
In this Demonstration, the recent population history is visualized as a trajectory on a triangular simplex: close proximity to one of its vertices signals that a large share of the total population belongs to the species indicated next to the vertex. How close the system is to its maximum carrying capacity is shown by the slider below the simplex.
Initially the population consists of an equal number of As, Bs, and Cs. As no species is favored in this situation, the trajectory remains at the fixed point in the simplex center until random deviations push it toward one of the corners. Having orbited around the simplex center—corresponding to the oscillations of the different species—the trajectory will reach an edge when one species becomes extinct. It will then approach the vertex of the winning species and stay there forever.
You can set the initial conditions by clicking into the simplex or dragging the population slider, or use the sliders to the left of the simplex to change the overall rates at which selection and reproduction occur. By choosing the "instant reproduction" option, you can couple both processes so that As directly replace dead Bs, Bs replace dead Cs, and Cs replace dead As. Instant reproduction keeps the total population count at the initial value and slows down the outward movement of the trajectory because species with a large population share are now less likely to profit from deaths in other subpopulations than in the original case.
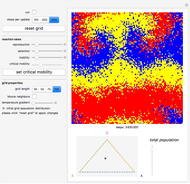
The spiral patterns that emerge when a spatial version of this scenario is played out on a grid lattice are shown in another Demonstrations project, "Biodiversity in Spatial Rock-Paper-Scissors Games".
References: B. Kerr, M. A. Riley, M. W. Feldman, and B. J. M. Bohannan, "Local Dispersal Promotes Biodiversity in a Real-Life Game of Rock-Paper-Scissors," Nature, 418, 2002 pp. 171–174. B. Sinervo and C. M. Lively, "The Rock-Scissors-Paper Game and the Evolution of Alternative Male Strategies," Nature, 380, 1996 pp. 240-243. T. Reichenbach, M. Mobilia, and E. Frey, "Coexistence versus Extinction in the Stochastic Cyclic Lotka-Volterra Model," Phys. Rev. E, 74(5), 2006. T. Reichenbach, M. Mobilia, and E. Frey, "Self-Organization of Mobile Populations in Cyclic Competition," J. Theor. Biol., 254(2), 2008 pp. 368–383.
Permanent Citation
"Stochastic Rock-Paper-Scissors Population Dynamics"
http://demonstrations.wolfram.com/StochasticRockPaperScissorsPopulationDynamics/
Wolfram Demonstrations Project
Published: March 7 2011