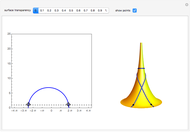
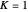Surfaces of Revolution with Constant Gaussian Curvature

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
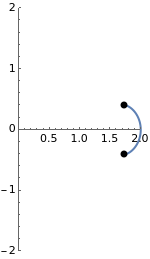
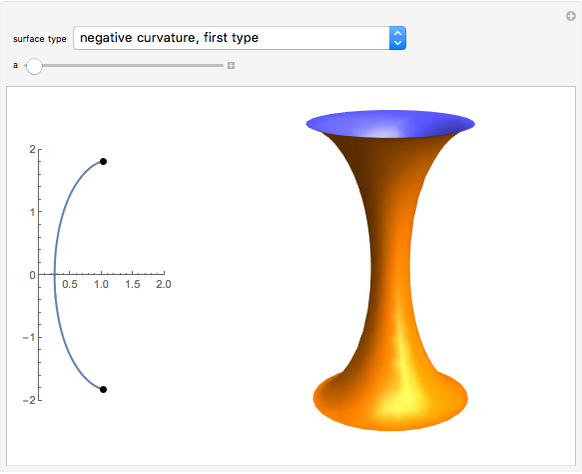
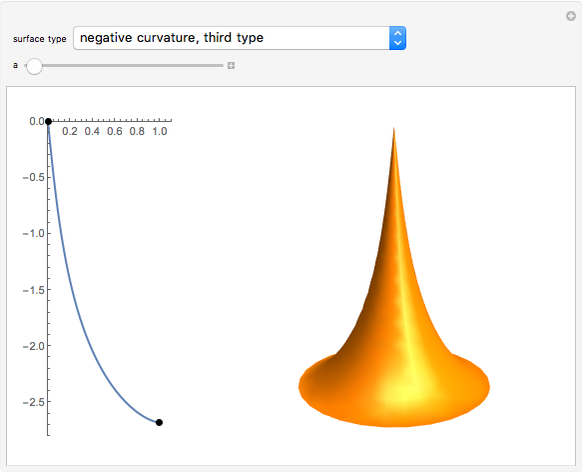
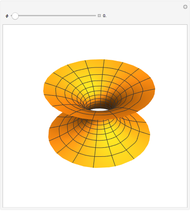
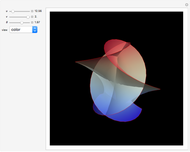
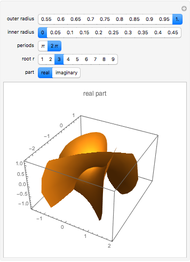
A surface of revolution arises by rotating a curve in the  -
- plane around the
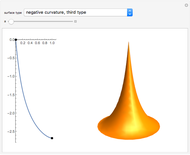
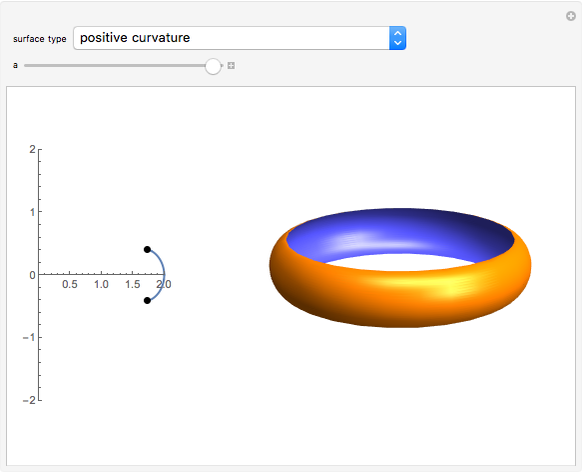
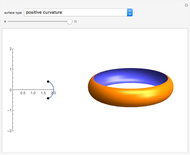
plane around the  axis. This Demonstration lets you explore the surfaces of revolution with constant nonzero Gaussian curvature
axis. This Demonstration lets you explore the surfaces of revolution with constant nonzero Gaussian curvature 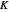 . Without loss of generality, we restrict ourselves to surfaces with
. Without loss of generality, we restrict ourselves to surfaces with 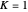 and
and 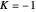 (other curvatures are obtained by an appropriate scaling).
(other curvatures are obtained by an appropriate scaling).
Contributed by: Antonin Slavik (May 2011)
(Charles University, Prague)
Open content licensed under CC BY-NC-SA
Snapshots
Details
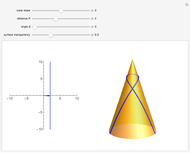
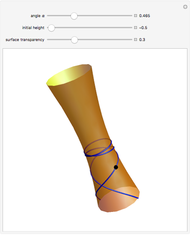
Assume that the profile curve 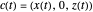 is parametrized by arc length, that is,
is parametrized by arc length, that is, 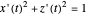 . Gaussian curvature of the corresponding surface of revolution
. Gaussian curvature of the corresponding surface of revolution  is then given by
is then given by  . Since
. Since  is a constant, we obtain a second-order differential equation
is a constant, we obtain a second-order differential equation 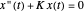 . This equation is easy to solve analytically; the corresponding function
. This equation is easy to solve analytically; the corresponding function  is then calculated from the first equation by numerical integration.
is then calculated from the first equation by numerical integration.
See, for example, Section 5.7 in [1] or Chapter 3 of [2].
References
[1] B. O’Neill, Elementary Differential Geometry, 2nd ed., London: Elsevier Academic Press, 2006.
[2] M. Spivak, A Comprehensive Introduction to Differential Geometry, Vol. 3, 3rd ed., Houston: Publish or Perish, 1999.
Permanent Citation