Tacoma Narrows Bridge Collapse

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
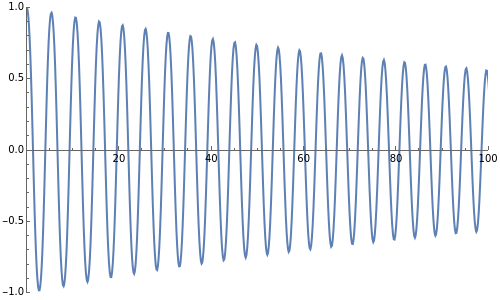
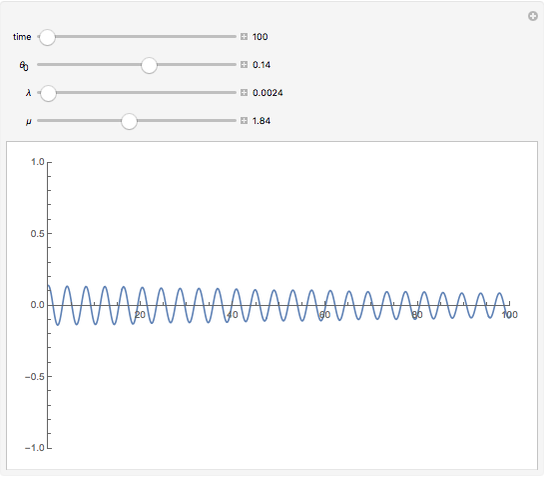
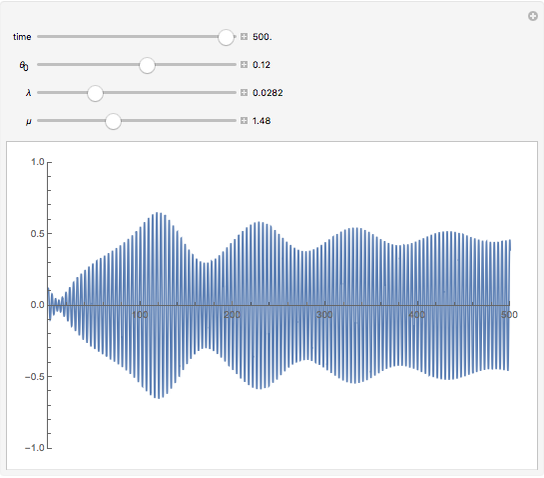
On November 7, 1940, the Tacoma Narrows Bridge collapsed. An explanation based on resonance was offered at that time, but in 1990, a new model was considered [1]. Assuming that a cable cannot be described with the usual Hooke's law, it set up a nonlinear model with vertical and torsional motion. This Demonstration uses another equation presented in 1999 [2] that avoided linearizing the torsional equation to avoid removing a wide variety of behavior. A sinusoidal forcing term was introduced with amplitude  and frequency
and frequency  , while
, while 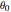 corresponds to the initial angle. Cases with slight increases for small torsional forcing with a transitioning to large oscillations can be observed, which is what presumably happened at Tacoma Narrows.
corresponds to the initial angle. Cases with slight increases for small torsional forcing with a transitioning to large oscillations can be observed, which is what presumably happened at Tacoma Narrows.
Contributed by: Enrique Zeleny (August 2011)
Open content licensed under CC BY-NC-SA
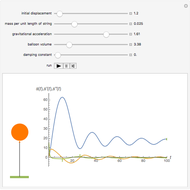
Snapshots
Details
For the torsional motion, the equation and the initial conditions are
 .
.
References
[1] A. C. Lazer and P. J. McKenna, "Large Amplitude Periodic Oscillations in Suspension Bridges: Some New Connections with Nonlinear Analysis," SIAM Review, 32(4), 1990 pp. 537–578.
[2] P. J. McKenna, "Large Torsional Oscillation in Suspension Bridges Revisited: Fixing an Old Approximation," American Mathematical Monthly, 106(1), 1999 pp. 1–18.
[3] Tacoma Narrows Bridge Collapse "Gallopin' Gertie" [Video]. Retrieved August 16, 2011, from http://www.youtube.com/watch?v=j-zczJXSxnw.
Permanent Citation