Taylor Expansions with Noninteger Number of Terms

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
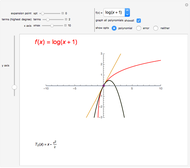
At regular points 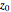 , an analytic function
, an analytic function 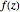 can be expanded in a series of the form
can be expanded in a series of the form 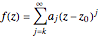 . In case it is possible to obtain a closed form of the truncated series
. In case it is possible to obtain a closed form of the truncated series 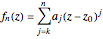 as an analytic function of
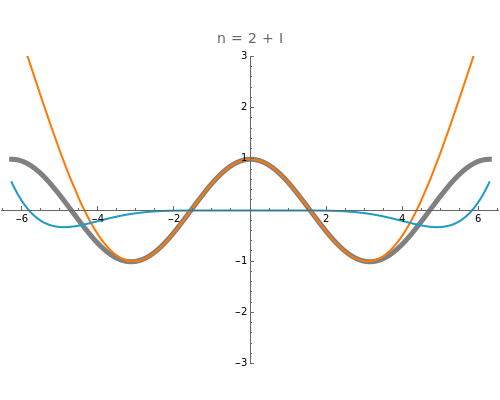
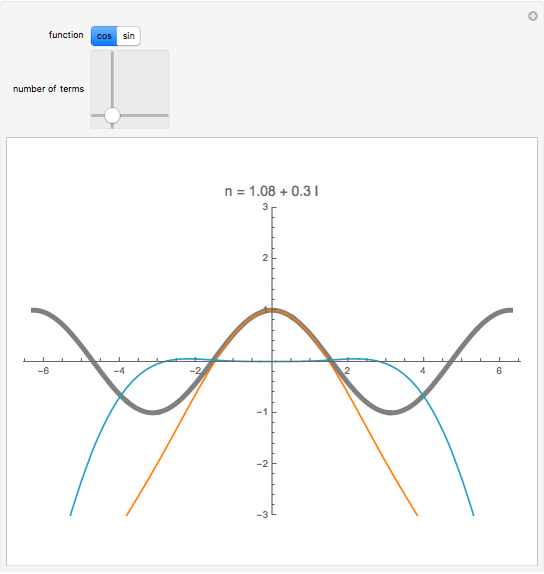
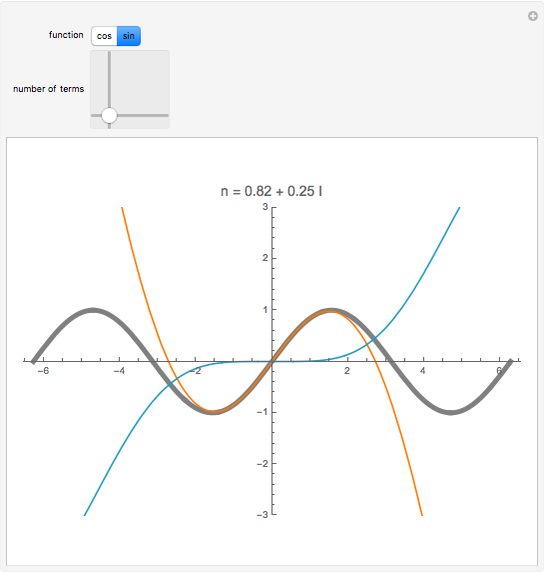
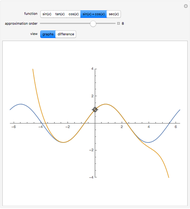
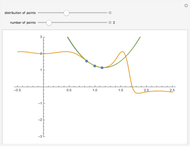
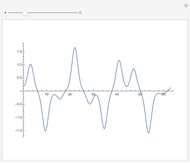
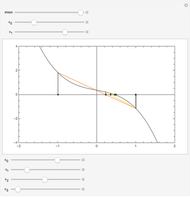
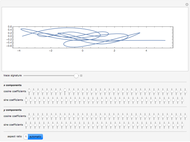
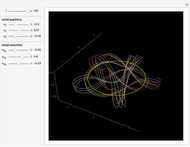
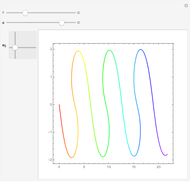
as an analytic function of  , we can consider this to be a natural continuation of the Taylor series to an noninteger (even complex) number of terms. This Demonstration plots these continuations for the functions cosine and sine. The gray curve is the original function; the orange and blue curves are the real and imaginary parts of the analytic continuation.
, we can consider this to be a natural continuation of the Taylor series to an noninteger (even complex) number of terms. This Demonstration plots these continuations for the functions cosine and sine. The gray curve is the original function; the orange and blue curves are the real and imaginary parts of the analytic continuation.
Contributed by: Michael Trott (March 2011)
Open content licensed under CC BY-NC-SA
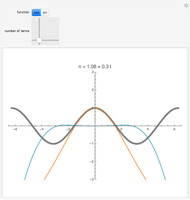
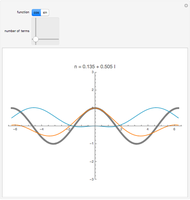
Snapshots
Details
function — the trigonometric function to be used number of terms — the number of terms of the Taylor expansion to take into account
Permanent Citation
"Taylor Expansions with Noninteger Number of Terms"
http://demonstrations.wolfram.com/TaylorExpansionsWithNonintegerNumberOfTerms/
Wolfram Demonstrations Project
Published: March 7 2011