The 1860 US Presidential Election under Different Voting Methods

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
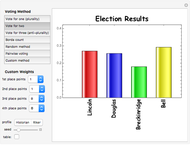
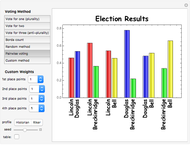
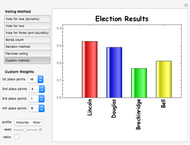
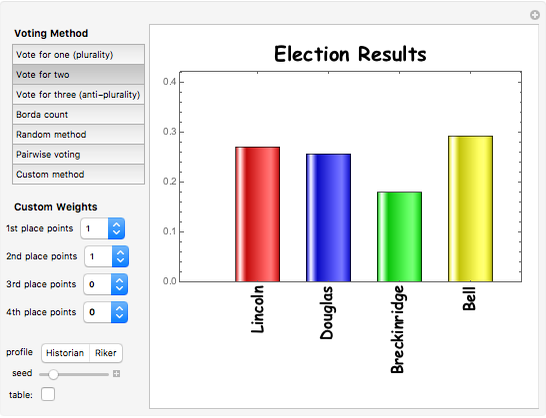
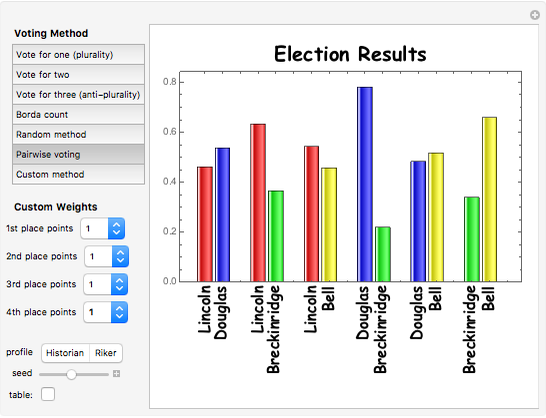
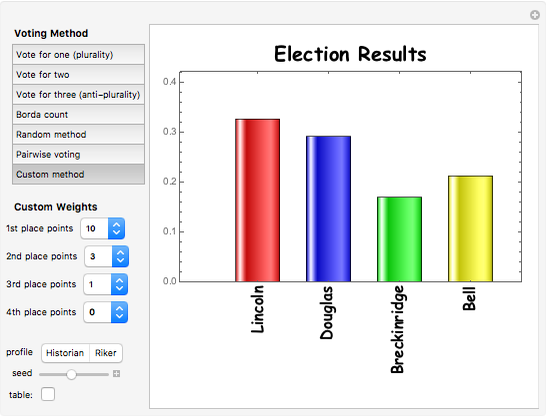
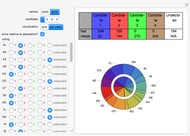
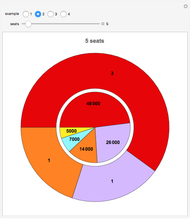
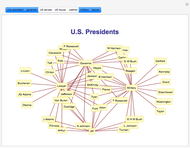
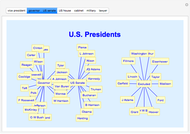
The 1860 US presidential election, in which Abraham Lincoln was elected by plurality vote, was one of the most important elections in the history of the United States. This Demonstration shows how the outcome of the election would have been affected if different voting methods had been used. To see the results in tabular form, check the "table" box.
Contributed by: Zelin Li and A. J. Hildebrand (February 2016)
Based on an undergraduate research project at the Illinois Geometry Lab by Daoyu Duan, Zelin Li, Yukun Tan, and
Mengzhou Tang, directed by Matthew Romney and A. J. Hildebrand
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration is based on an analysis by Tabarrok and Spector [2] (see also Saari [1]) of outcomes of the 1860 US presidential election under different voting methods. In arriving at these results, the authors used estimates of voter preferences provided by 13 prominent historians (the "Historian" profile) and by the political scientist William Riker (the "Riker" profile). The results are slightly different depending on which of these profiles is used.
The Demonstration shows, for each of these two profiles, the election results under the following voting methods:
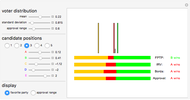
Vote for one: Each voter votes for one of the four candidates. This is the usual plurality method.
Vote for two: Each voter votes for exactly two of the four candidates.
Vote for three: Each voter votes for exactly three of the four candidates. This is the anti-plurality method.
Borda count: In this method, the highest-ranked candidate by a voter receives 3 points, the second-highest 2 points, the third-highest 1 point, and the lowest-ranked candidate 0 points. The winner is determined by the total number of points received by each candidate.
Custom/random methods: These are generalizations of the Borda count method, with the number of points for first, second, third, and fourth places specified by the user or chosen randomly.
Pairwise voting: In this method, the four candidates are compared pairwise. A candidate who wins all pairwise comparisons is the Condorcet winner of the election.
References
[1] D. G. Saari, Chaotic Elections! A Mathematician Looks at Voting, American Mathematical Society, 2001 pp. 33–69.
[2] A. Tabarrok and L. Spector, "Would the Borda Count Have Avoided the Civil War?" Journal of Theoretical Politics, 11(2), 1999 pp. 261–288.
Permanent Citation
"The 1860 US Presidential Election under Different Voting Methods"
http://demonstrations.wolfram.com/The1860USPresidentialElectionUnderDifferentVotingMethods/
Wolfram Demonstrations Project
Published: February 25 2016