The Aging Spring

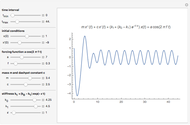
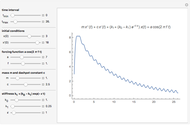
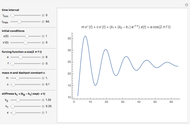
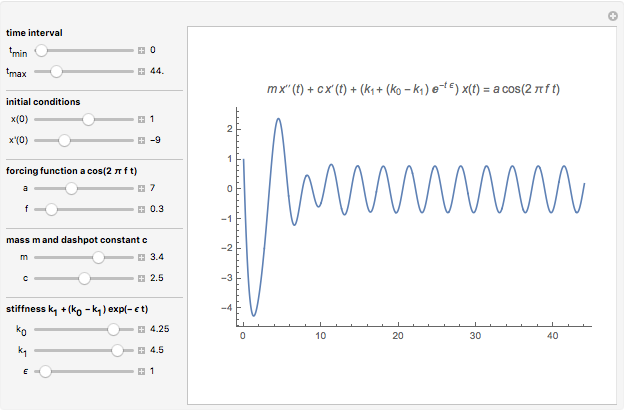
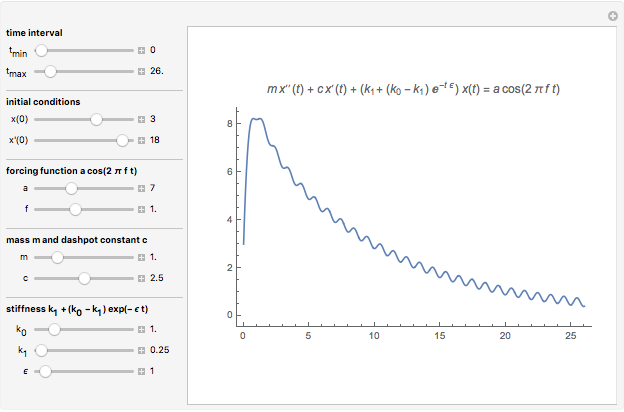
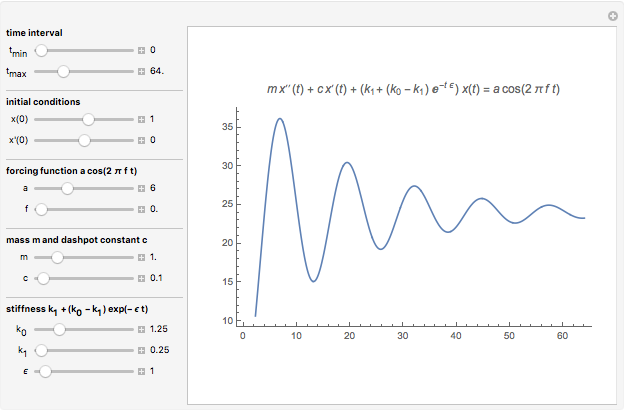
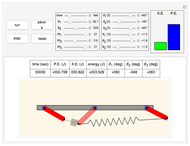
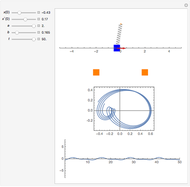
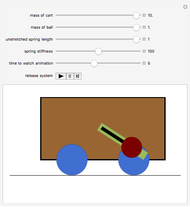
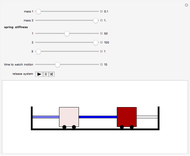
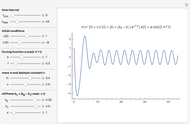
The dynamical system governed by the following time-varying ordinary differential equation is a variation of the classic forced mass-spring-dashpot system with mass , dashpot constant , constant stiffness , and forcing term . Aging springs are characterized by a stiffness decaying with time. Here an exponential decay from an initial value at time zero to an asymptotic value is considered.

Mathematica can integrate this equation exactly, but the solution in general is a huge expression involving BesselJ and Gamma functions, together with their integrals; it is very difficult to imagine their behavior as time advances.