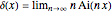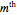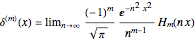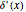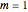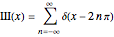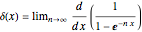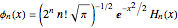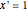Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

The Deltafunction as the Limit of Some Special Functions

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

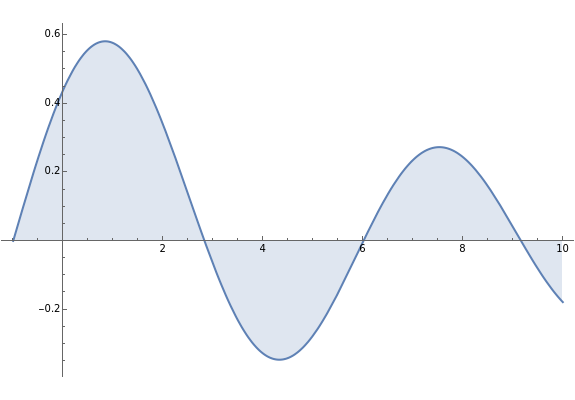
Another Demonstration gives some representations for the Dirac deltafunction as the limit of elementary functions (see the related links below).This Demonstration illustrates several additional limiting relations involving special functions and the deltafunction:

[more]

Bessel: , (

Airy: .

Hermite: The derivative of the deltafunction is given by . Shown is with .

Dirichlet kernel: , where the delta-comb or shah function is defined by . This is a periodic extension of the deltafunction.

Fejér kernel: , with the same periodicity as the Dirichlet kernel.

Sigmoid: The derivative of the sigmoid function: .

Closure: An orthonormal set of functions {} obeys the closure relation . This is shown for orthonormalized Hermite functions with .

[less]

Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

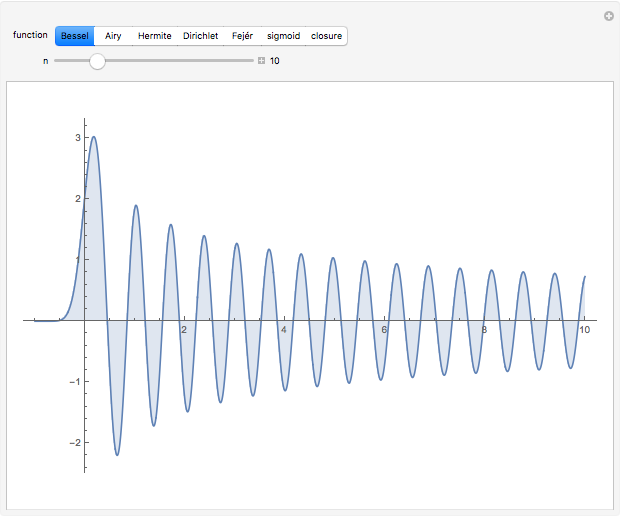
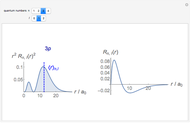
Snapshot 1: Bessel function representation with All but the leftmost peak will produce canceling contributions as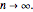

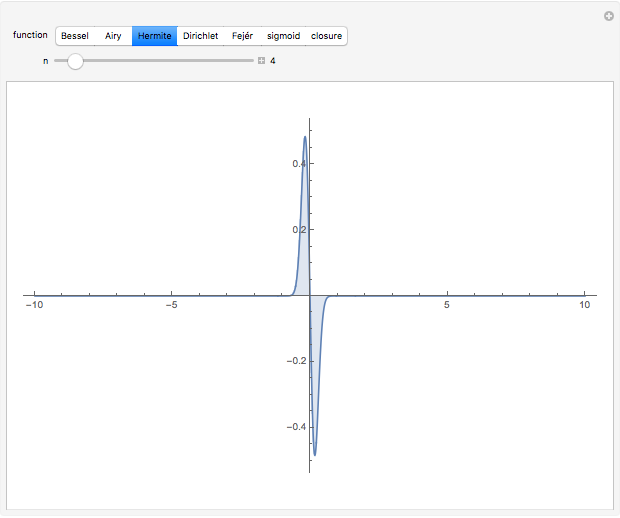
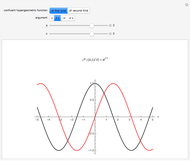
Snapshot 2: approach to 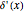using Hermite polynomial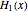

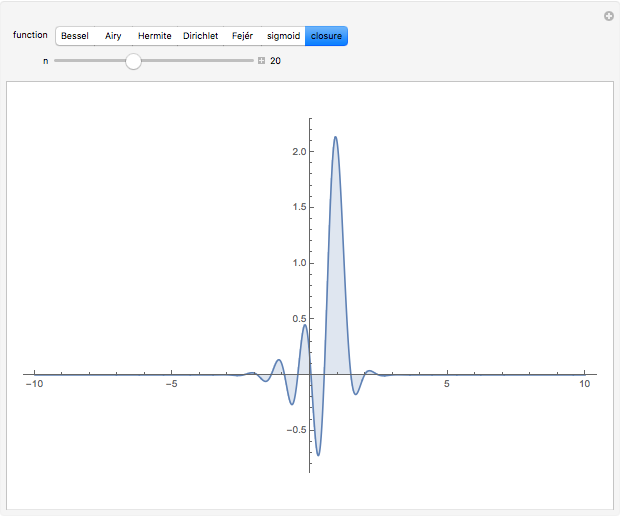
Snapshot 3: closure relation approaching

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send