The Iterated Prisoner's Dilemma

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
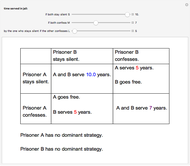
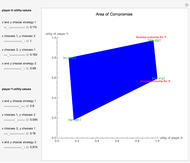
The prisoner's dilemma is a two-player game in which each player (prisoner) can either "cooperate" (stay silent) or "defect" (betray the other prisoner). If both players cooperate, they each get a reward 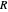 ; if both defect, they will receive a punishment payoff
; if both defect, they will receive a punishment payoff 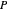 ; if one player defects and the other cooperates, the defecting player receives a temptation payoff
; if one player defects and the other cooperates, the defecting player receives a temptation payoff 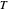 , while the cooperating player receives a sucker payoff
, while the cooperating player receives a sucker payoff 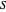 . In the standard form of the game,
. In the standard form of the game, 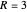 ,
, 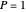 ,
, 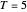 and
and 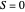 .
.
Contributed by: HaeJin Lee (June 2020)
Open content licensed under CC BY-NC-SA
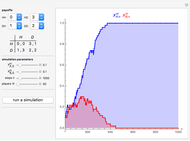
Snapshots
Details
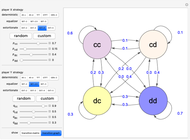
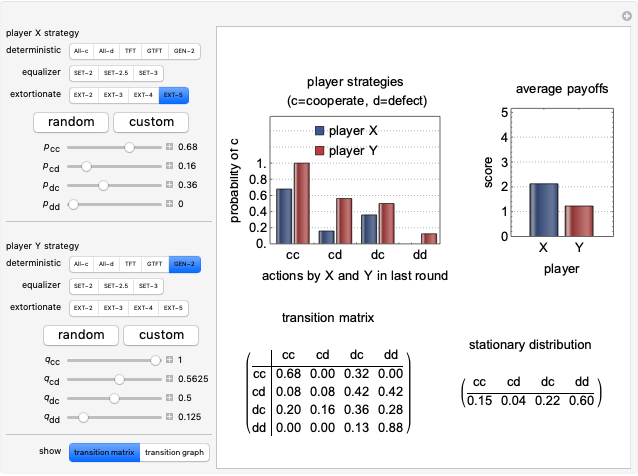
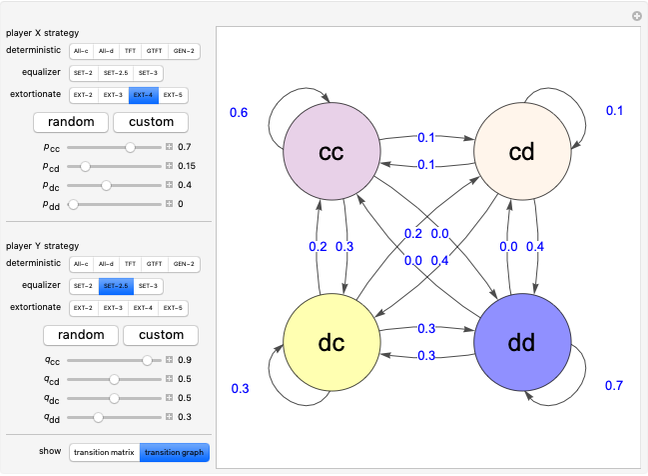
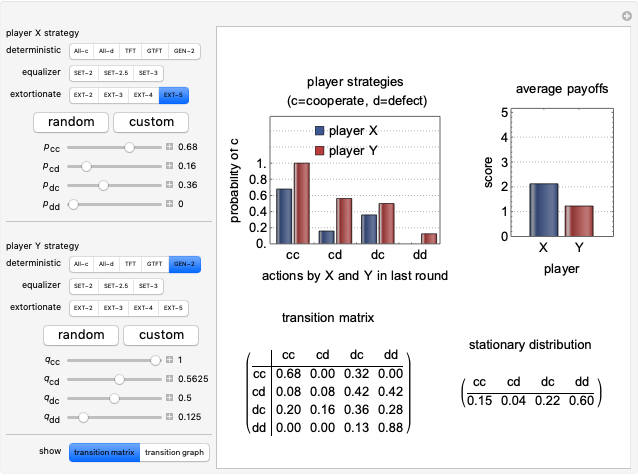
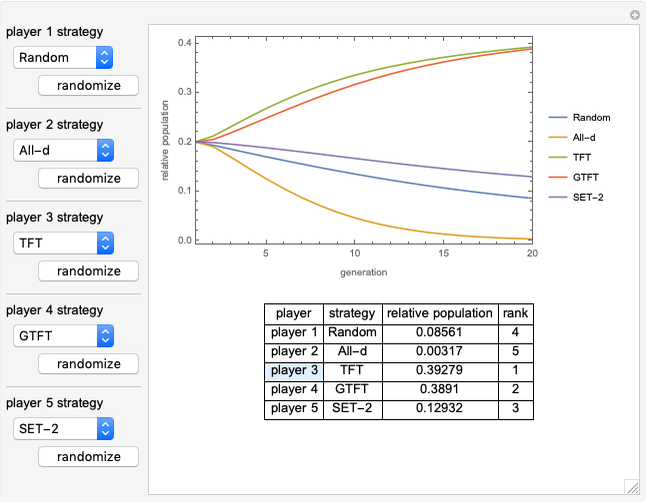
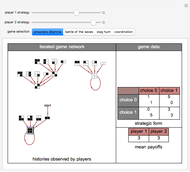
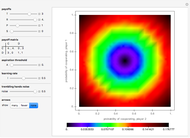
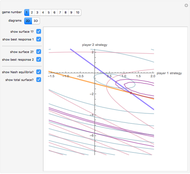
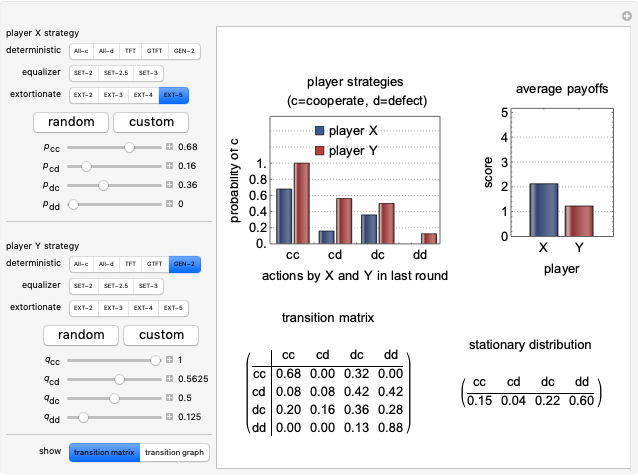
Memory-one strategies in the IPD are determined by a strategy vector 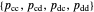 whose components represent the probabilities that the player cooperates given a particular pair of actions by the two players in the previous round. These strategies can be modeled by a Markov chain on the four states cc, cd, dc, dd (see [3]). In this demonstration, player X's strategy vector is defined as
whose components represent the probabilities that the player cooperates given a particular pair of actions by the two players in the previous round. These strategies can be modeled by a Markov chain on the four states cc, cd, dc, dd (see [3]). In this demonstration, player X's strategy vector is defined as 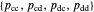 , and player Y's strategy vector is defined as
, and player Y's strategy vector is defined as 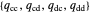 .
.
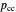 represents the probability of cooperating by player X if both players cooperated in the previous round.
represents the probability of cooperating by player X if both players cooperated in the previous round.
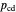 represents the probability of cooperating by player X if player X cooperated and player Y defected in the previous round.
represents the probability of cooperating by player X if player X cooperated and player Y defected in the previous round.
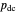 represents the probability of cooperating by player X if player X defected and player Y cooperated in the previous round.
represents the probability of cooperating by player X if player X defected and player Y cooperated in the previous round.
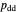 represents the probability of cooperating by player X if both players defected in the previous round.
represents the probability of cooperating by player X if both players defected in the previous round.
The  are like the
are like the 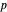 .
.
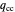 represents the probability of cooperating by player Y if both players cooperated in the previous round.
represents the probability of cooperating by player Y if both players cooperated in the previous round.
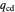 represents the probability of cooperating by player Y if player Y cooperated and player X defected in the previous round.
represents the probability of cooperating by player Y if player Y cooperated and player X defected in the previous round.
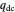 represents the probability of cooperating by player Y if player Y defected and player X cooperated in the previous round.
represents the probability of cooperating by player Y if player Y defected and player X cooperated in the previous round.
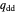 represents the probability of cooperating by player Y if both players defected in the previous round.
represents the probability of cooperating by player Y if both players defected in the previous round.
Controls
All-c: the player always cooperates. Strategy vector 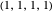 .
.
All-d: the player always defects. Strategy vector 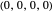 .
.
TFT (tit for tat [2]): the player cooperates if the opponent cooperated in the previous round and defects if the opponent defected in the previous round. Strategy vector 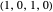 .
.
GTFT (generous tit for tat [2]): the player cooperates after every instance of an opponent’s cooperation and after 25% of the opponent’s defections. Strategy vector 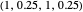 .
.
GEN-2 (generous zero-determinant strategy [2]): strategy vector 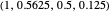 .
.
SET (equalizer strategies [1, 3]): a family of strategies that set payoffs for the opponent. For example, SET-2 forces the opponent’s payoff to be 2 regardless of what strategy the opponent uses. Strategy vectors: SET-2: 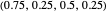 ; SET-2.5:
; SET-2.5: 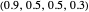 ; SET-3:
; SET-3: 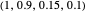 .
.
EXT (extortionate strategies [1, 3]): a family of strategies that guarantees the player a higher or equal payoff no matter what the opponent does. Strategy vectors: EXTORT-2: 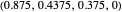 ; EXTORT-3:
; EXTORT-3: 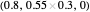 ; EXTORT-4:
; EXTORT-4: 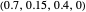 ; EXTORT-5:
; EXTORT-5: 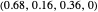 .
.
References
[1] C. Hilbe, M. A. Nowak and K. Sigmund, "Evolution of Extortion in Iterated Prisoner’s Dilemma Games," Proceedings of the National Academy of Sciences, 110(17), 2013 pp. 6913–6918. doi:10.1073/pnas.1214834110.
[2] S. Kuhn. "Prisoner's Dilemma." The Stanford Encyclopedia of Philosophy. (May 7, 2020) plato.stanford.edu/entries/prisoner-dilemma.
[3] W. H. Press and F. J. Dyson, "Iterated Prisoner’s Dilemma Contains Strategies That Dominate Any Evolutionary Opponent," Proceedings of the National Academy of Sciences, 109(26), 2012 pp. 10409–10413. doi:10.1073/pnas.1206569109.
Permanent Citation