Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

The Law of the Iterated Logarithm in Probability Theory

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

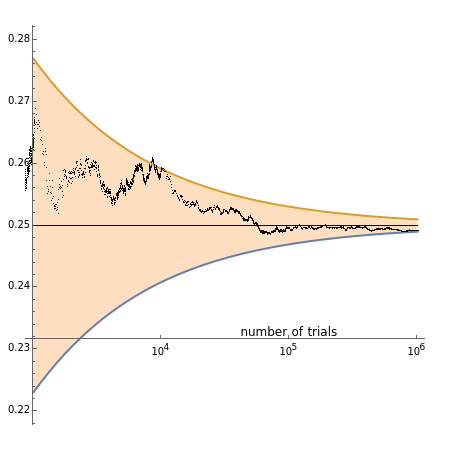
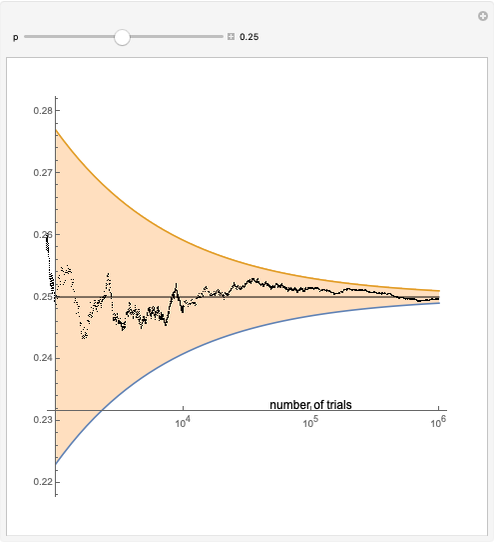
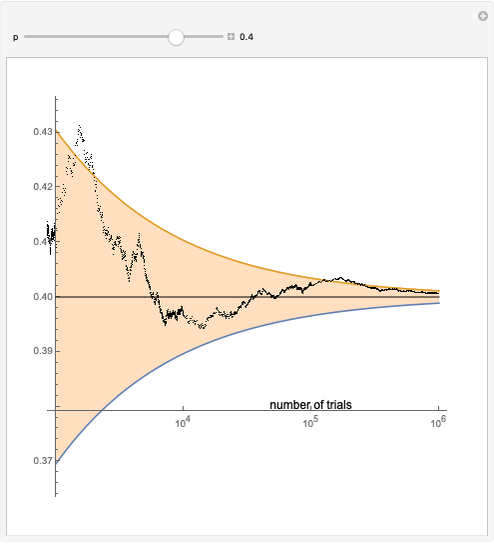
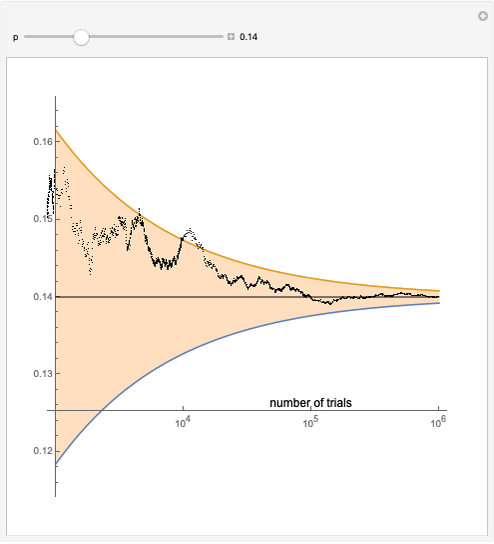
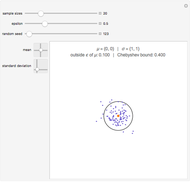
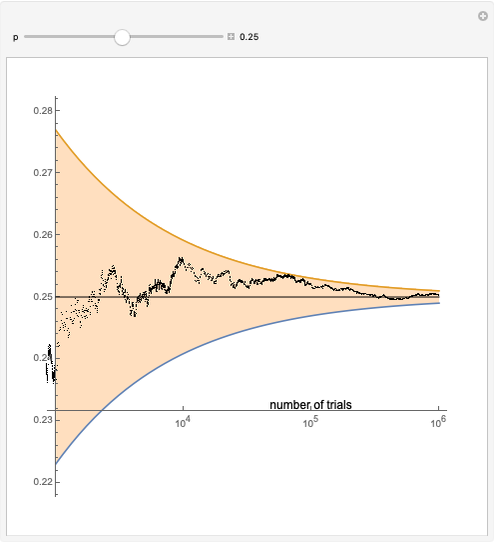
The law of the iterated logarithm is a refinement of the strong law of large numbers, a fundamental result in probability theory. In the particular case of an unlimited sequence of Bernoulli trials with parameter , the strong law asserts that with probability one, the relative frequency of successes converges to p as the number of trials grows.

[more]

The relative frequency of successes is simulated for 1,000,000 trials, and is plotted against a log scale for the number of trials. As the number of trials increases the relative frequency is observed to remain within the funnel-shaped region described by the law of the iterated logarithm, and only in rare cases will it land outside the funnel.

Move the slider to change the value of p and watch the behavior of the relative frequencies as a function of the number of trials. Open the control for the slider and use the "Play" animation control to repeat the process automatically for different values of .

[less]

Contributed by: Tomas Garza (December 2007)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The main reference for this topic is W. Feller, "Unlimited Sequences of Bernoulli Trials: The Law of the Iterated Logarithm," An Introduction to Probability Theory and Its Applications, Vol. 1, New York: John Wiley & Sons, Inc., 1970 pp. 204–208.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send