The Period of Lunar Tides

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
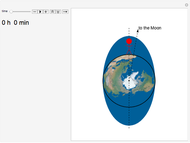
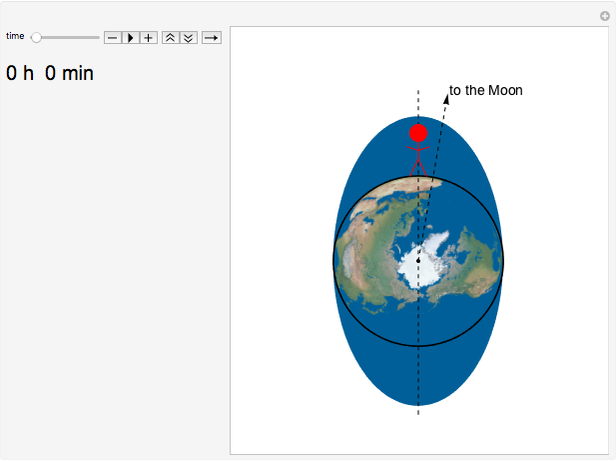
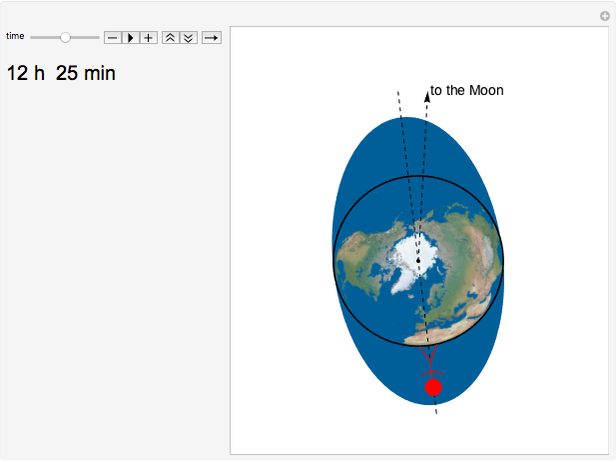
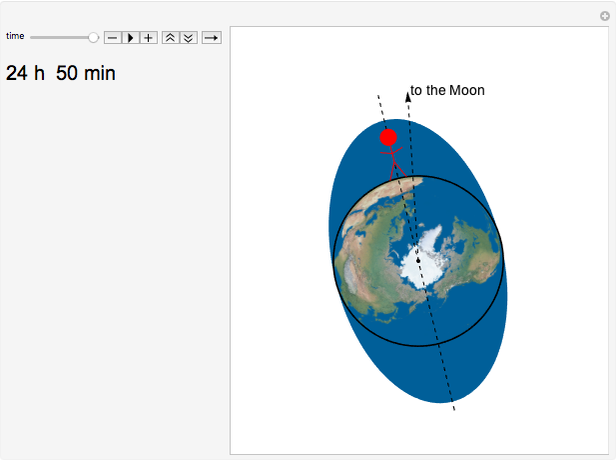
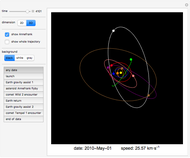
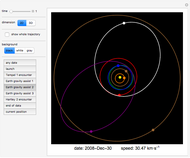
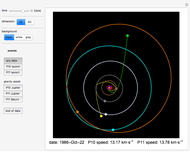
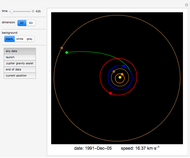
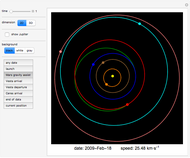
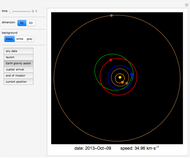
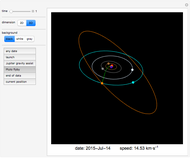
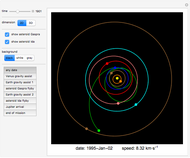
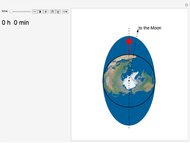
The period of tides is not exactly one day but a little bit longer, because the Moon orbits the Earth with a different period than the Earth rotates around its axis. We usually think that "the high tide is coming," but for an observer who is not standing on the Earth (as in the view of this Demonstration), observers on Earth are are actually going into the high tide.
Contributed by: Tomas Franc (April 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Suppose that the whole Earth is covered by water, and the Moon orbits the Earth above the equator.
The period of the tides  can be determined as the solution of the equation
can be determined as the solution of the equation
 ,
,
where  is the Earth's sidereal rotation period (around its axis), which is 23 h 56 min, and
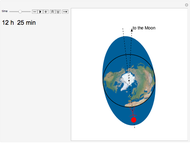
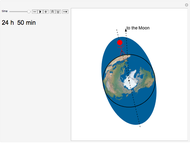
is the Earth's sidereal rotation period (around its axis), which is 23 h 56 min, and  is the Moon's revolution period around the Earth (the sidereal month), which is 27 d 7 h 43 min. The solution of this equation is 24 h 50 min, and because there are two water bulges, the high tide or low tide occurs every 12 h 25 min (the so-called semidiurnal tide), and the water level changes every 6 h 12 min.
is the Moon's revolution period around the Earth (the sidereal month), which is 27 d 7 h 43 min. The solution of this equation is 24 h 50 min, and because there are two water bulges, the high tide or low tide occurs every 12 h 25 min (the so-called semidiurnal tide), and the water level changes every 6 h 12 min.
Because of the Earth's continents, the high tides do not occur when the Moon is right above us (or right "under" us). The Sun also has an influence on the tides, the solar tidal force being approximately 2.2 smaller than the lunar. When we take into account all these effects (and some others not mentioned here), the high tide is slightly ahead of the connecting line between the centers of the Earth and the Moon (in the animation the angle is shown as 10° to make this fact obvious).
Permanent Citation