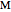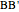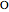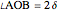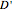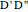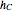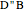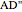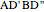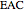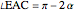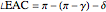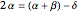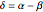The Plemelj Construction of a Triangle: 12
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
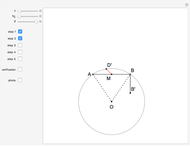
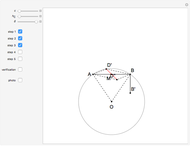
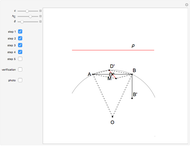
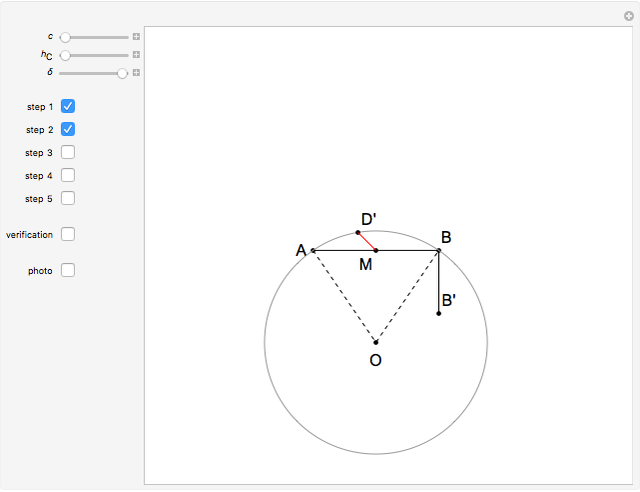
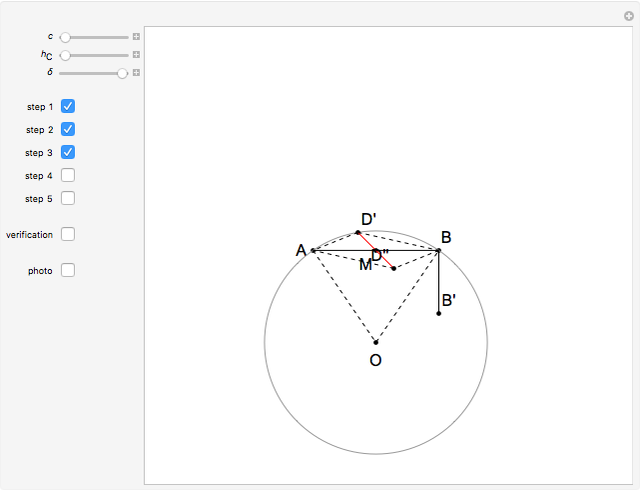
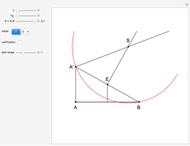
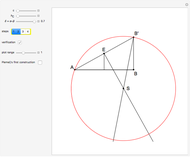
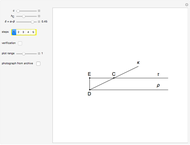
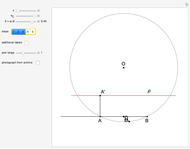
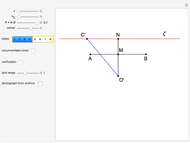
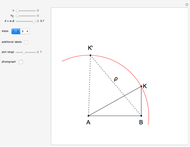
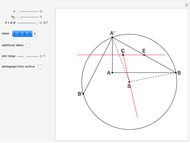
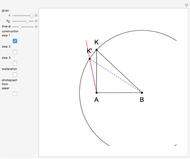
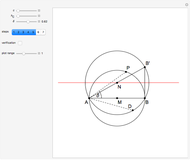
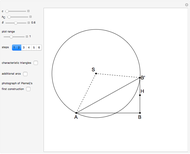
This Demonstration constructs a triangle 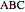 given the length
given the length  of its base
of its base 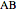 , the length
, the length 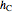 of the altitude from
of the altitude from  to
to 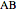 , and the difference
, and the difference  between the angles
between the angles  at
at 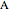 and
and 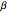 at
at 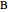 . This construction is an alternative to The Plemelj Construction of a Triangle: 5.
. This construction is an alternative to The Plemelj Construction of a Triangle: 5.
Contributed by: Izidor Hafner (September 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For the history of this problem, references and a photograph of Plemelj's first solution, see The Plemelj Construction of a Triangle: 1.
Permanent Citation