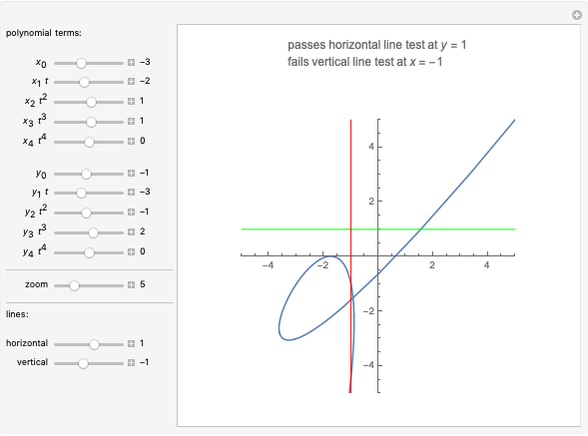
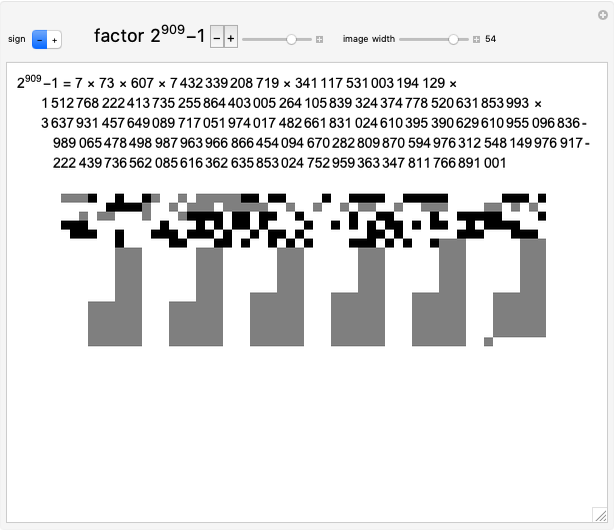
The Set of Sets in SET
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
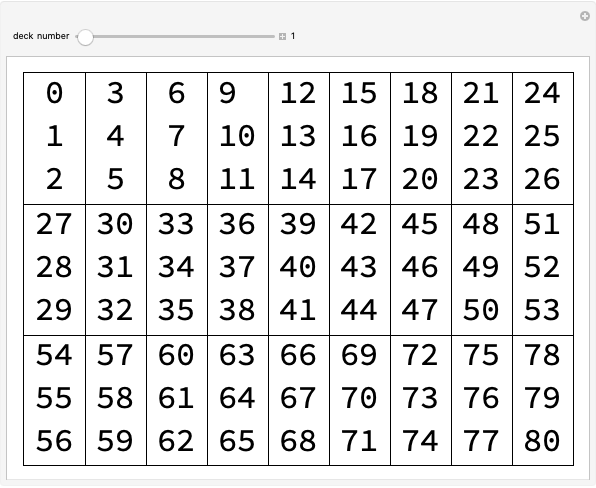
BitXor gives the bitwise XOR of a set of integers in binary form. This uses the finite field  . Is there something similar for
. Is there something similar for  ?
?
Contributed by: Ed Pegg Jr (February 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] Wikipedia. "Projective Plane." (Feb 7, 2020) en.wikipedia.org/wiki/Projective_plane.
[2] Wikipedia. "Set (Card Game)." (Feb 7, 2020) en.wikipedia.org/wiki/Set_(card_game).
Permanent Citation