The Sum of the Trilinear Coordinates of a Point
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
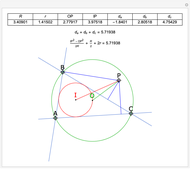
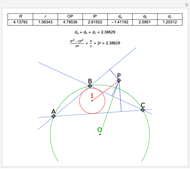
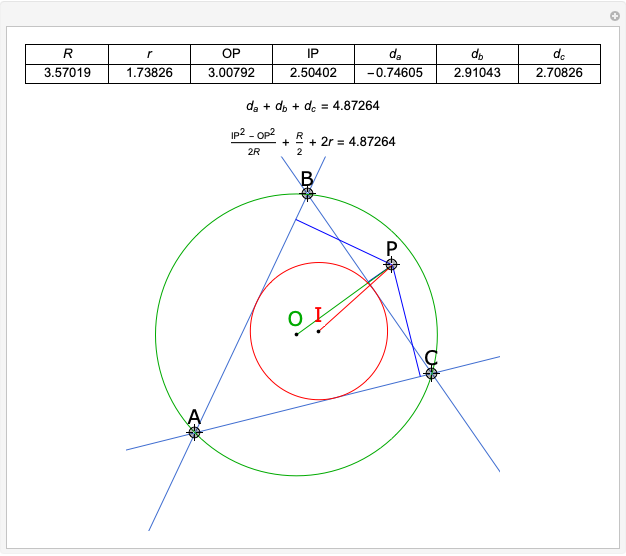
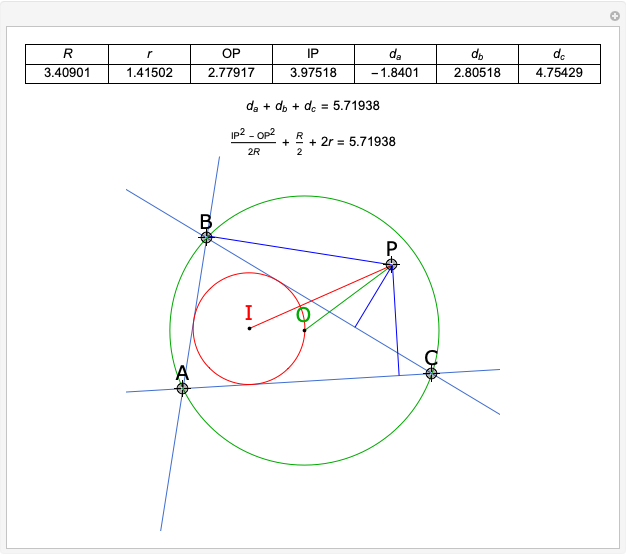
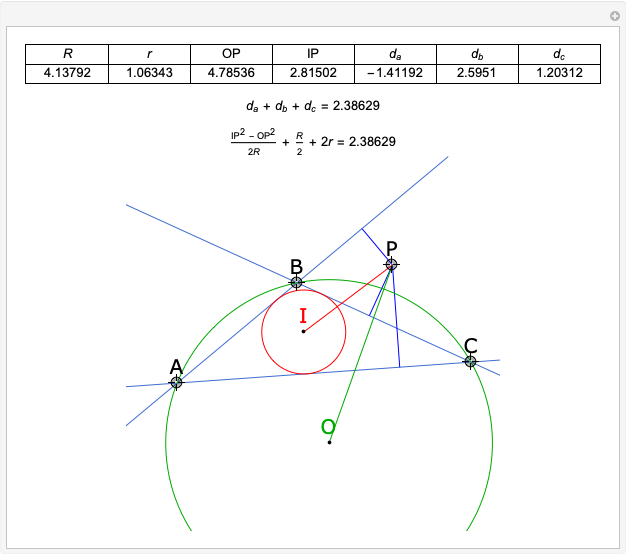
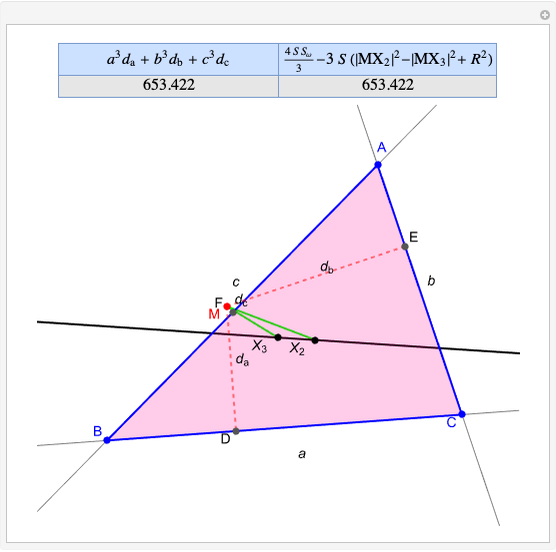
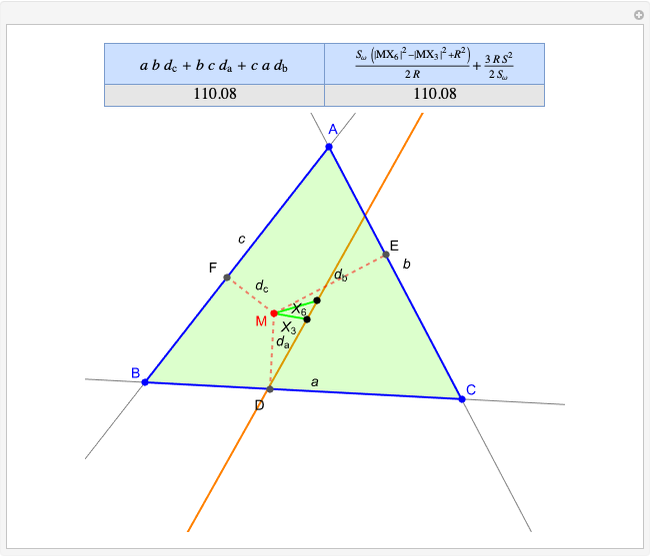
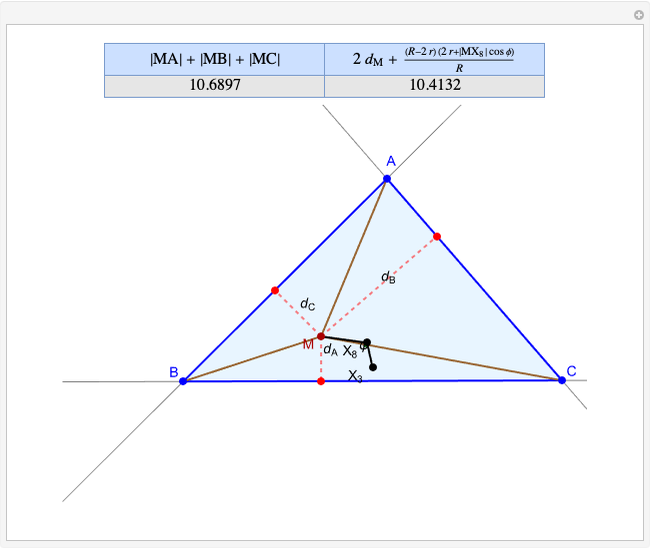
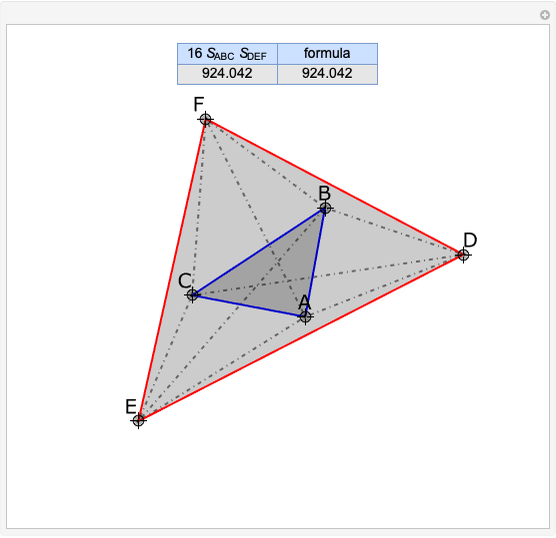
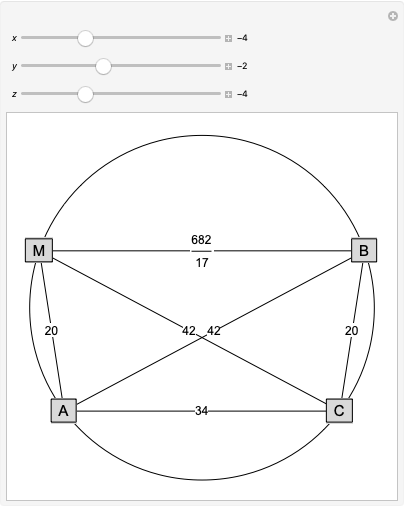
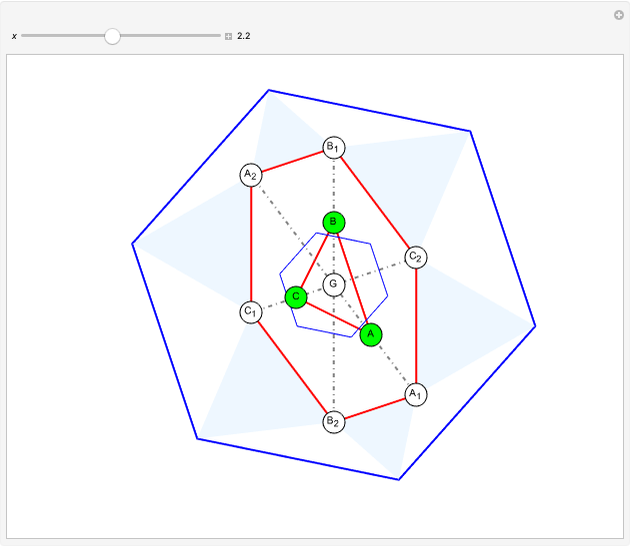
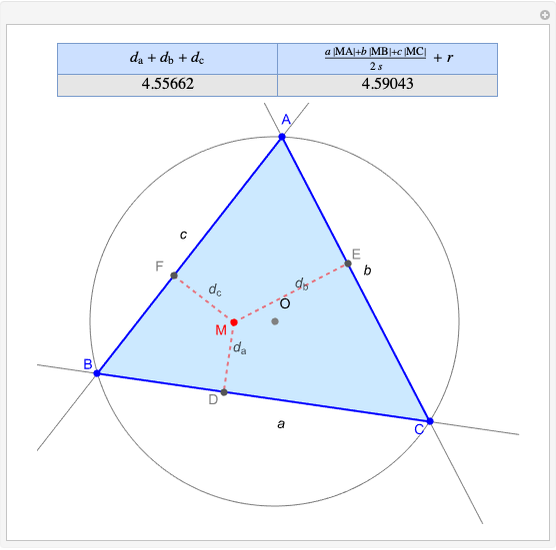
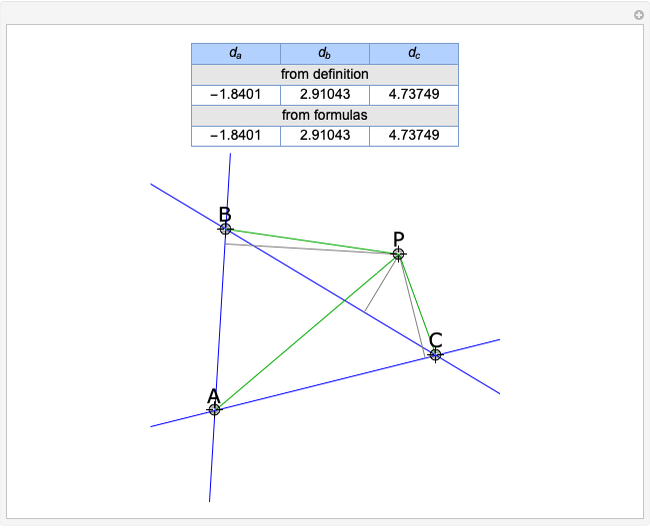
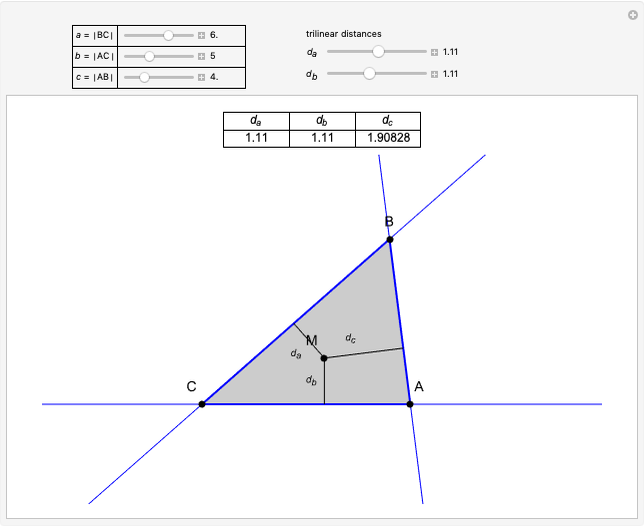
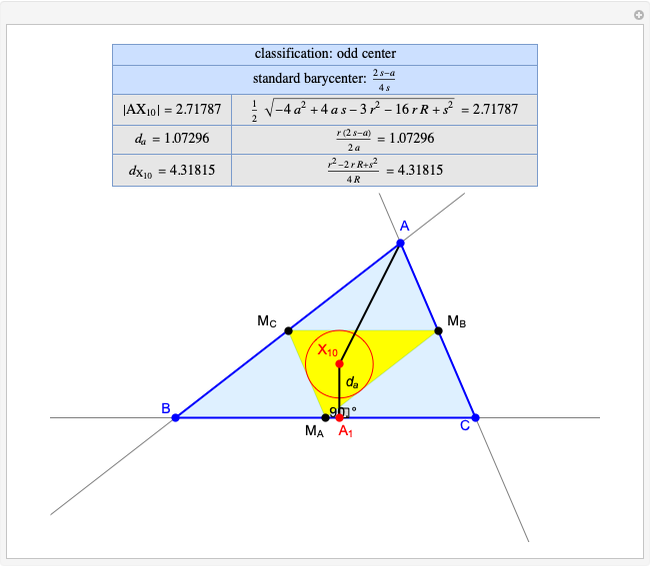
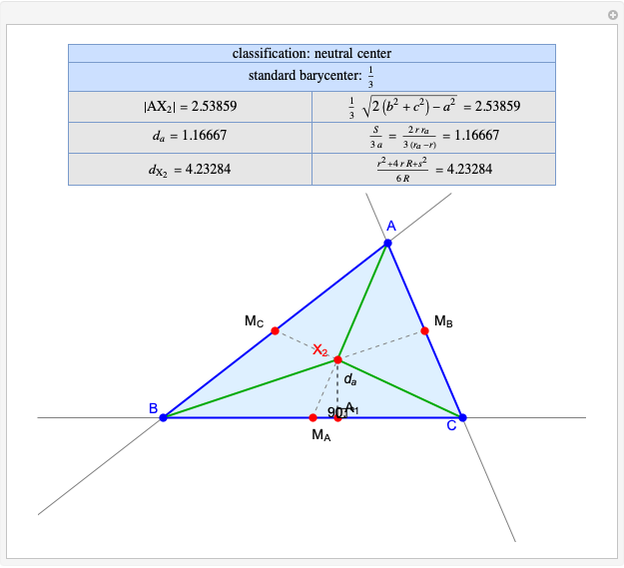
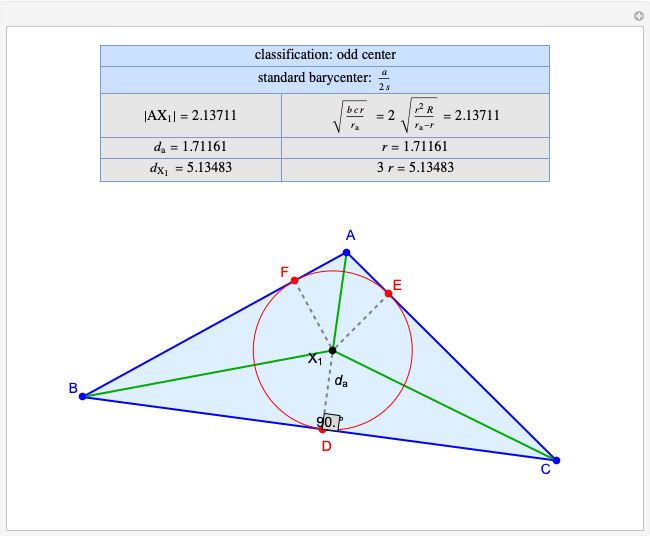
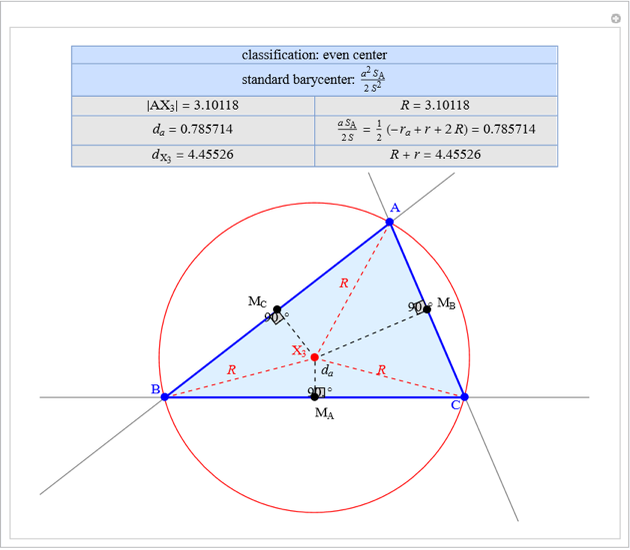
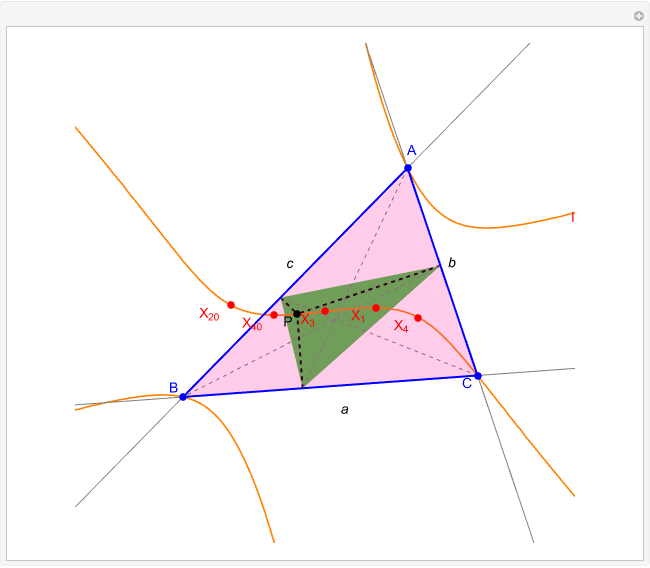
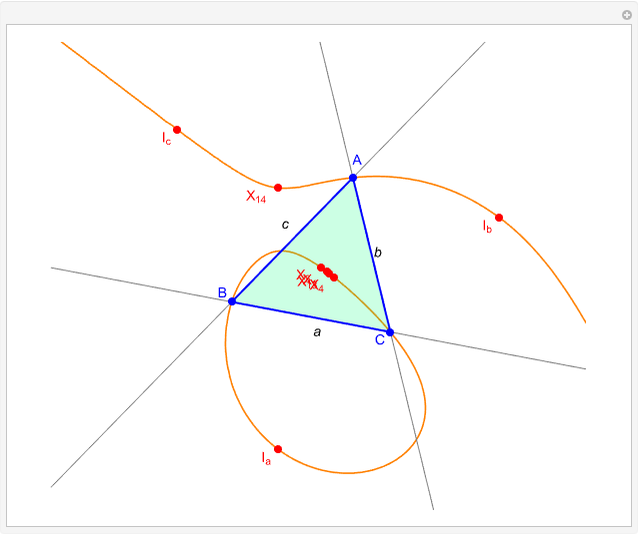
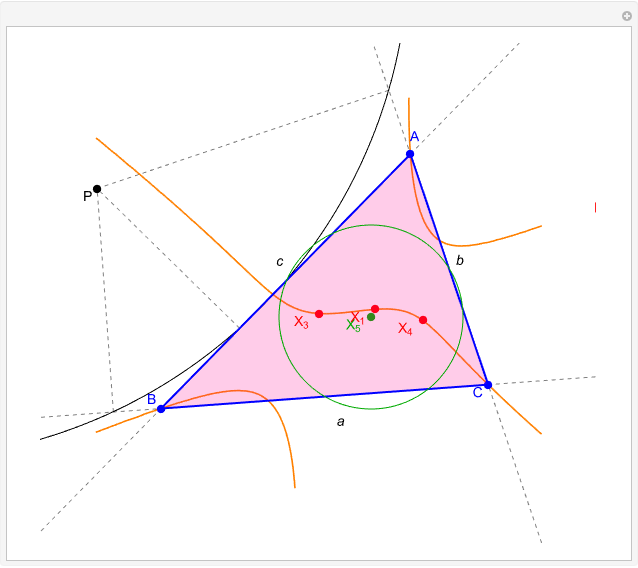
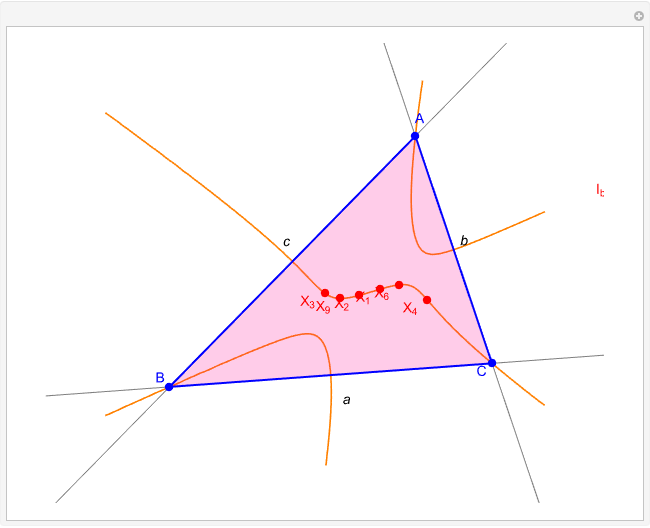
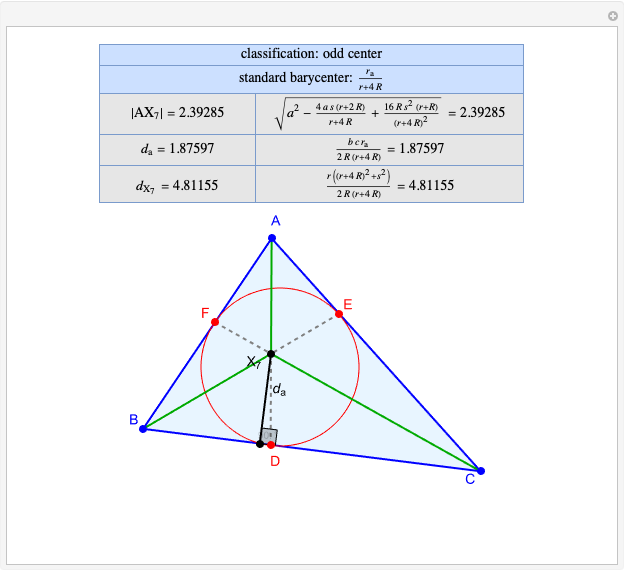
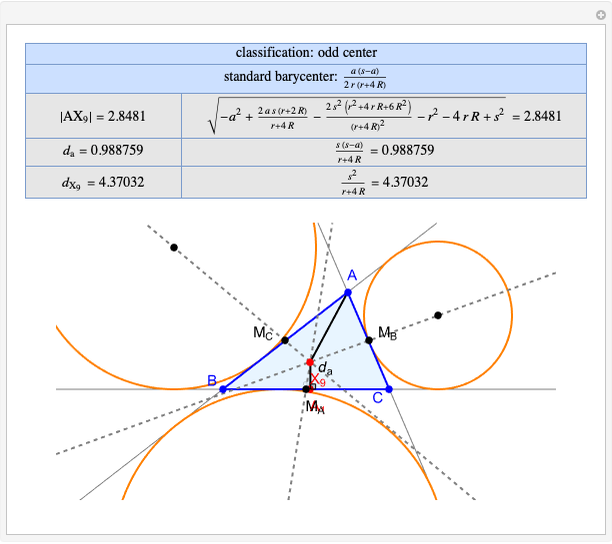
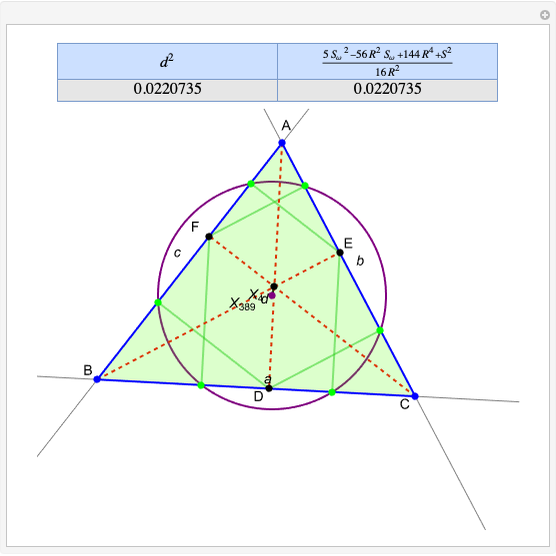
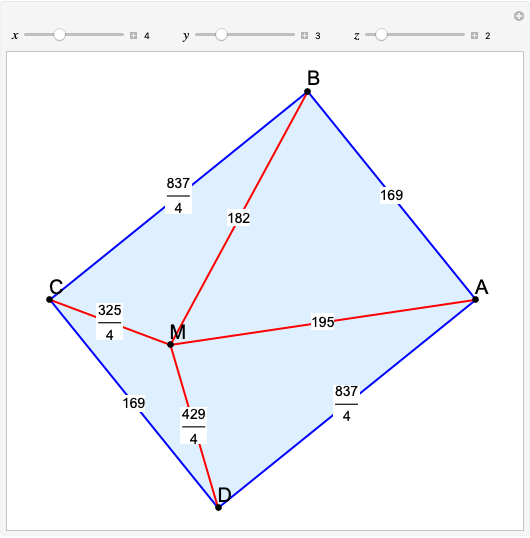
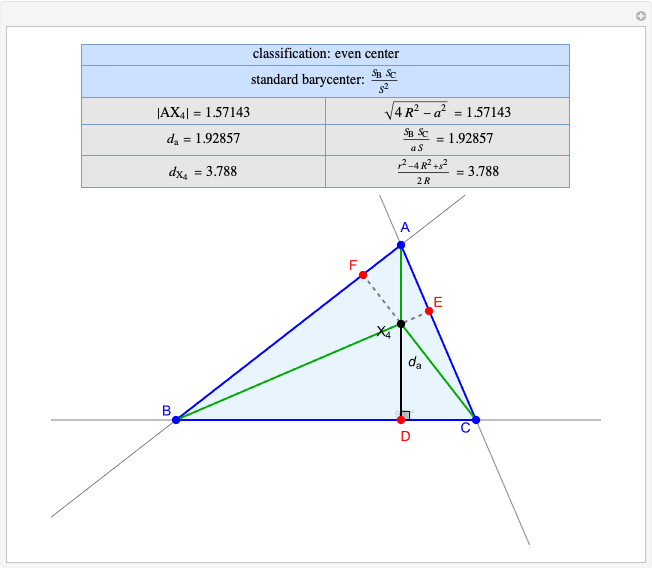
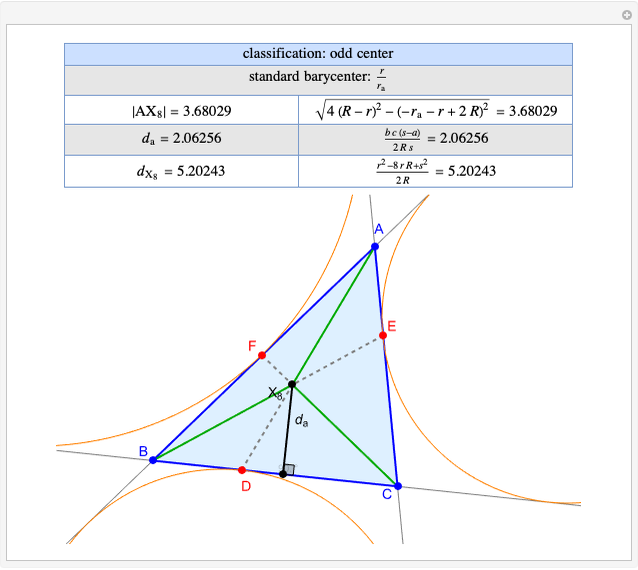
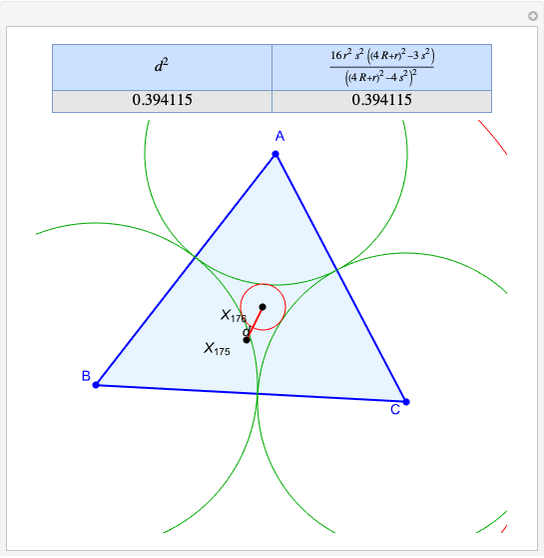
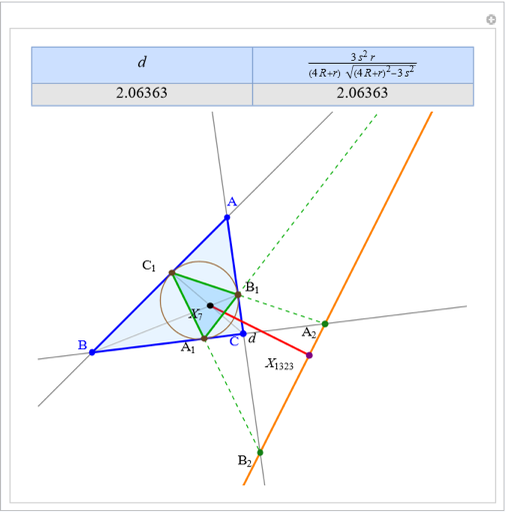
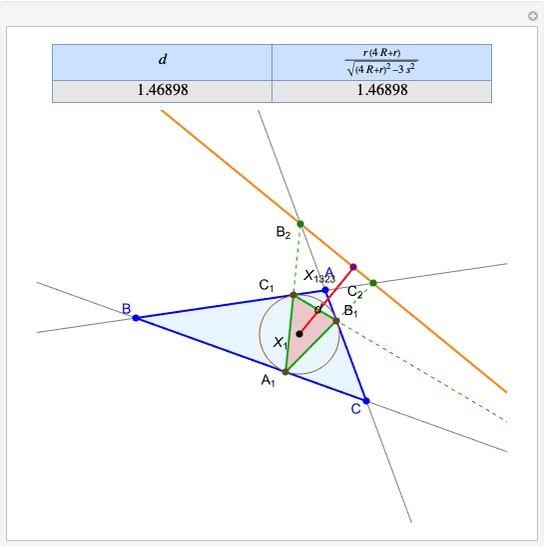
Given a triangle  , the trilinear coordinates of a point
, the trilinear coordinates of a point  are the signed distances to the extended sides. Denote the signed distances of
are the signed distances to the extended sides. Denote the signed distances of  to
to  ,
,  and
and 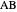 by
by  ,
,  and
and  , respectively. If
, respectively. If  and the incenter
and the incenter  are in the same half-plane determined by a side, the signed distance to that side is positive; otherwise, it is negative.
are in the same half-plane determined by a side, the signed distance to that side is positive; otherwise, it is negative.
Contributed by: Minh Trinh Xuan (August 2022)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation