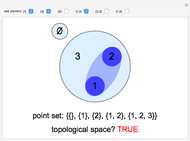
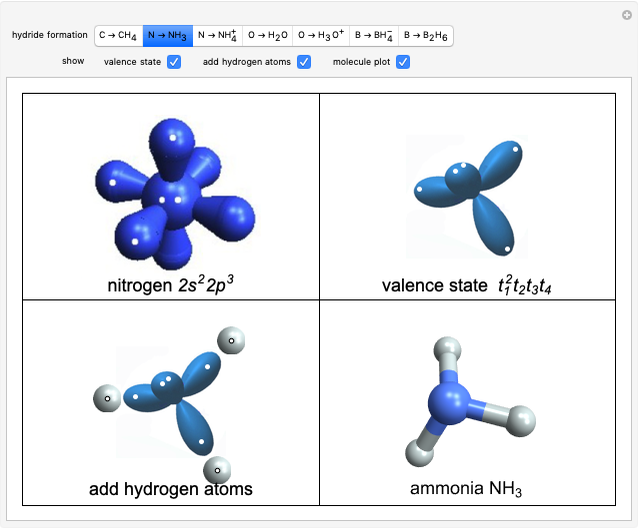
The Venturi Effect

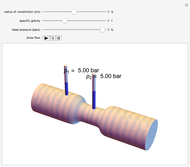
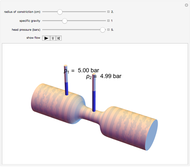
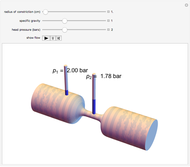
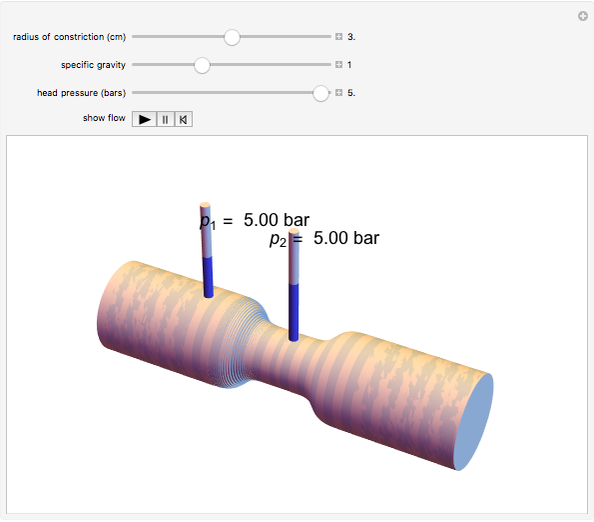
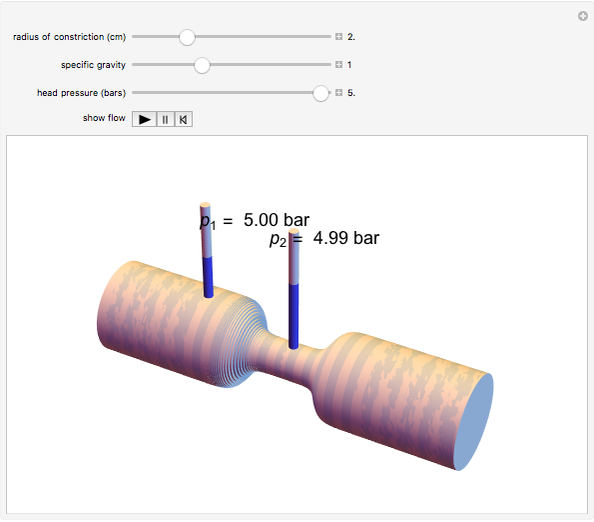
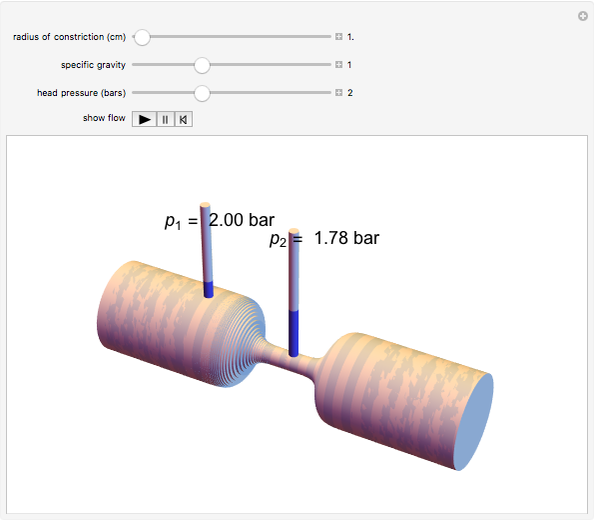
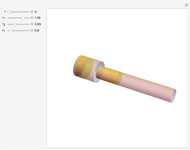
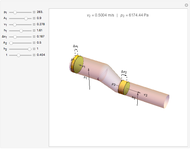
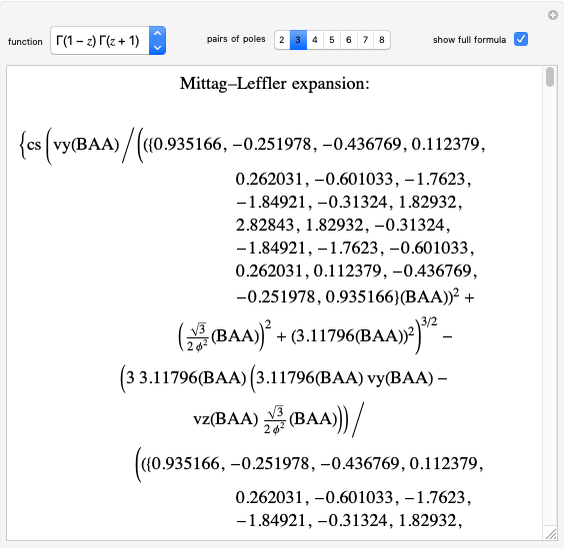
A fluid flowing through a constricted section of a tube undergoes a decrease in pressure, which is known as the Venturi effect. This is fundamentally a consequence of Bernoulli's principle, which relates the pressure of a fluid to its velocity , :

,

where is the density, assumed constant for an incompressible fluid. The equation of continuity determines the velocity of a fluid of given density through a section of tube with radius . You can vary the radius of the constriction between 1 and 5 cm. Quantitative details depend on additional factors, such as the viscosity of the fluid and the roughness of the tube walls. The results given in this Demonstration can be considered as representative.

The drop of fluid pressure is indicated by the difference in fluid levels in the two vertical capillary tubes. The Venturi-tube flowmeter operates on this principle.