Three Parametrizations of Rotations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
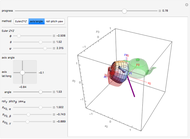
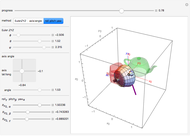
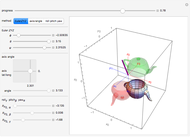
A rotation can be parameterized in several ways. This Demonstration compares three popular parametrizations:
[more]
Contributed by: Aaron T. Becker and Benedict Isichei (September 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
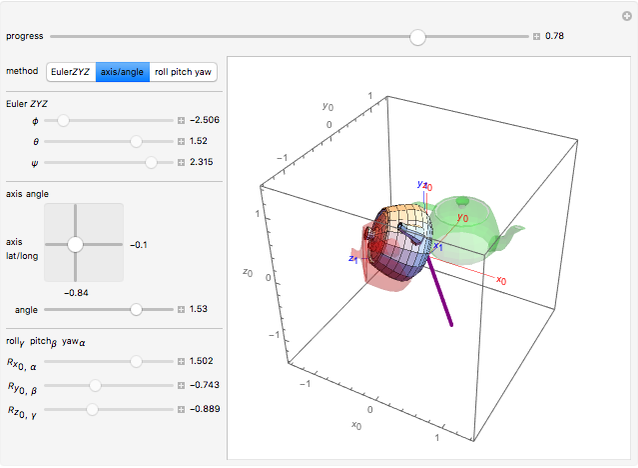
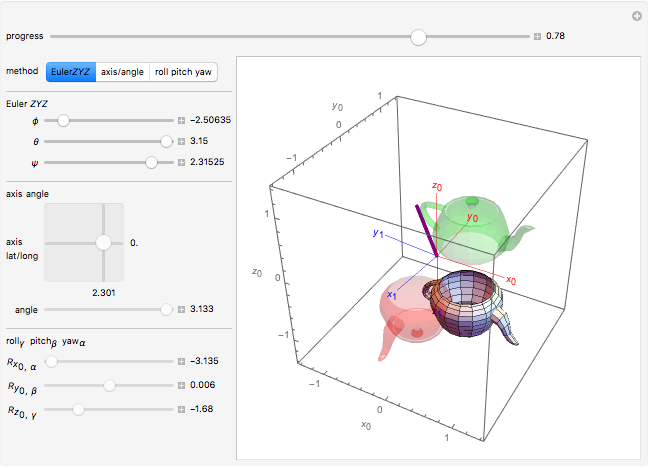
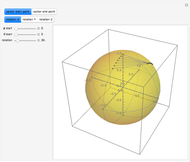
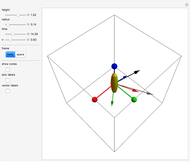
This Demonstration shows three parametrizations to describe rotations between a fixed coordinate frame 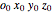 and a rotated frame
and a rotated frame  .
.
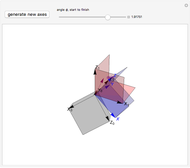
The first parametrization uses Euler angles. There are many Euler angle conventions. This Demonstration uses the 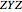 convention, which specifies the orientation of frame
convention, which specifies the orientation of frame  by three successive rotations. The first rotates about the
by three successive rotations. The first rotates about the  axis by the angle
axis by the angle  . Next, we rotate about the current
. Next, we rotate about the current  axis by the angle
axis by the angle  . Finally, we rotate about the current
. Finally, we rotate about the current  axis by the angle
axis by the angle  .
.
The composite rotation, using the shorthand convention of  for
for  and
and 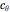 for
for 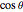 , is
, is
 .
.
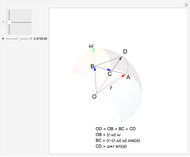
Euler's rotation theorem states that any combination of rotations of a rigid body, such that a point in the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. The second parametrization uses axis/angle parametrization, a rotation of  about the unit axis
about the unit axis 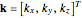 . This again gives only three parameters, by representing
. This again gives only three parameters, by representing 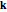 by the two-parameter latitude/longitude pair:
by the two-parameter latitude/longitude pair: 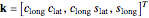 . Using the convention
. Using the convention  :
:
 .
.
The final parametrization uses roll, pitch, and yaw angles, denoted as  ,
,  and
and  . The order of rotation in this Demonstration is around the fixed coordinate frame
. The order of rotation in this Demonstration is around the fixed coordinate frame  axes: first, a yaw about
axes: first, a yaw about  through an angle
through an angle  ; second, a pitch about
; second, a pitch about  by an angle
by an angle  ; and third, a roll about
; and third, a roll about  by an angle
by an angle  . Because the rotations are about the fixed coordinate frame, the successive rotations pre-multiply, giving the composite rotation
. Because the rotations are about the fixed coordinate frame, the successive rotations pre-multiply, giving the composite rotation
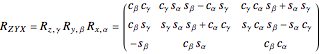 .
.
Reference
[1] M. W. Spong, S. Hutchinson and M. Vidyasagar, Robot Modeling and Control, Hoboken, NJ: John Wiley & Sons, 2006.
Permanent Citation